commons-math 解読 (13) : 複素数 Complex に定義されている複素関数　【多価関数編】

前回に引き続き、今回も Complex クラスに定義されている複素関数を見ていきます。　今回見ていくのは対数関数にはじまる多価関数。　これらはどれも偏角の取り得る値の多価に起因するものですが、角度の範囲を適切に制限することによって（主値をとることによって）一価関数として扱えるようになっています。

関数の定義

今回扱う関数の宣言：

public class Complex{
    ...

    // 対数関数
    Complex log()

    // 累乗
    Complex pow(Complex x)

    // 逆三角関数
    Complex asin()
    Complex acos()
    Complex atan()

    // 累乗根
    Complex sqrt()
    Complex sqrt1z()
    List<Complex> nthRoot(int n)
}

サンプル

サンプルコードをいくつか：

import static java.lang.Math.*

// 対数関数
assert new Complex(1d, 1d).log() == new Complex(log(2d)/2d, PI/4d)    // log(1 - i) = log2/2 + iπ/4
assert new Complex(1d, -1d).log() == new Complex(log(2d)/2d, -PI/4d)    // log(1 - i) = log2/2 - iπ/4

// 冪乗
assert Complex.I.pow(Complex.I) == new Complex(E**(-PI/2d), 0d)    // i^i = exp(-π/2)

// 逆三角関数
assert new Complex(-1d/sqrt(2d), 0d).asin() == new Complex(-PI/ 4d, 0d)    // asin(-1/√2) = -π/4
assert new Complex(-1d/sqrt(2d), 0d).acos() == new Complex(3d*PI/ 4d, 0d)    // acos(-1/√2) = 3π/4

// 平方根
assert Complex.ONE.sqrt() == Complex.ONE    // √1 = 1
assert Complex.ONE.negate().sqrt() == Complex.I    // √-1 = i
assert Complex.I.sqrt(), new Complex(1d/sqrt(2d) == 1d/sqrt(2d))    // √i = (1 + i)/√2
assert Complex.I.negate().sqrt(), new Complex(1d/sqrt(2d) == -1d/sqrt(2d))    // √-i = (1 - i)/√2
assert new Complex(-1d/2d, sqrt(3d)/2d).sqrt() == new Complex(1d/2d, sqrt(3d)/2d)
    // √(-1/2 + i√3/2) = 1/2 + i√3/2
assert new Complex(-1d/2d, -sqrt(3d)/2d).sqrt() == new Complex(1d/2d, -sqrt(3d)/2d)
    // √(-1/2 - i√3/2) = 1/2 - i√3/2

// 累乗根
def root4 =  [Complex.ONE, Complex.I, Complex.ONE.negate(), Complex.I.negate()]    // [1, i, -1, -i]
Complex.ONE.nthRoot(4).every{
    root4.contains(it)
}

対数関数 Logarithm Function

対数関数は指数関数の逆関数です。　引数の複素数 ${ z }$ の絶対値 ${ \left| z \right| }$ 、偏角 ${ \arg(z) }$ を用いて表すと

　　 $\log(z) = \log|z|+i\arg(z)$

となります。　引数の複素数 ${ z }$ の偏角 ${ \arg(z) }$ は ${ 2n\pi i\;(n\in \mathbf{Z}) }$

　　 $-\pi < \arg(z) \le \pi$

の範囲に制限されているため、一価関数として扱えます。

実部・虚部での表現

引数の複素数 ${ z }$ を ${ z = x + yi }$ （ ${ x,\,y }$ は実数）としたとき、 ${ \log(z) }$ の表式を ${ x,\,y }$ と実数関数で表すと

　　 ${ \displaystyle \begin{align*} \log(x + yi) &= \log\sqrt{x^2+y^2} + i \tan^{-1} \left(\frac{y}{x}\right) \\ &= \frac{1}{2}\log(x^2+y^2) + i \tan^{-1} \left(\frac{y}{x}\right) \end{align*} }$

となります。　ここで ${ \tan^{-1} }$ は ${ \tan }$ の逆関数です（arctan, atan と同じ）。

累乗　Power

複素数の累乗は

　　 $z^w = \exp(w\log z)$

によって定義、計算されます。　定義に対数関数が含まれているため累乗も多価となりますが、対数関数で返り値を一意に決めておけば、この累乗でも値を一意に決定できます。　ちなみに、サンプルに書いているコードは

　　 $i^i = (e^\frac{\pi i}{2})^i = e^{-\frac{\pi}{2}}$

を確かめてます。

逆三角関数 Inverse Trigonometric Functions

三角関数の逆関数、逆三角関数も多価関数です。　引数が実数の場合は、やはり角度の多価からくる ${ 2n\pi i \; (n \in \mathbf{Z}) }$

${ \sin\theta,\,\tan\theta }$ は ${ -\pi/2 \le \theta \le \pi/2 }$
${ \cos\theta }$ は ${ 0 \le \theta \le \pi }$

です：

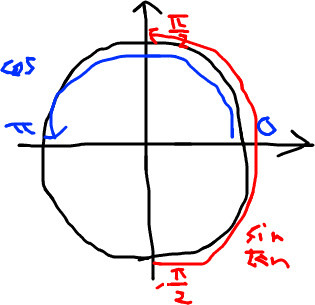
　引数が複素数の場合はもっと複雑ですが、これは累乗の場合と同じように対数関数 ${ \log z }$ の偏角の制限によって決定されます。　というのは、commons-math では（この分野では通常そうなのでしょうが）、逆三角関数も対数関数を用いて計算されるからです。　逆三角関数と対数関数との間には以下のような関係があります：

　　 ${ \displaystyle \begin{align*} \sin^{-1} z &= -i \log\left(\sqrt{1 - z^2} + iz \right) \\ \cos^{-1} z &= -i \log\left(z + i \sqrt{1 - z^2}\right) \\ \tan^{-1} z &= \frac{i}{2} \log\left(\frac{i + z}{i - z}\right) \end{align*} }$

導出は三角関数の指数関数による表現を用いればできます。　そのうち気が向けば。

平方根 Sqare Root

平方根は以下の式を使って計算されます：

　　 ${\rm sqrt}(x + yi) = \sqrt{\frac{r + x}{2}} \pm i\sqrt{\frac{r - x}{2}}\qquad(r = \sqrt{x^2+y^2})$

ここで、複合 ± は引数の複素数の虚部 (y) の符号と一致させます。　この表式は三角関数の半角の公式を用いて導けます。　返り値の複素数の偏角が取り得る値は

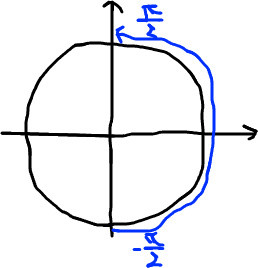
となってます。

Complex クラスに定義されている sqrt1z 関数は、上記の平方根を返す関数 sqrt() を用いて

　　 ${\rm sqrt1z}(z) = \sqrt{1-z^2}$

を計算します。　これは逆三角関数を計算するのに便利なので定義されているんでしょう。

累乗根 nth Root

最後は累乗根を返す関数。　この関数に対応するメソッドは、上記の平方根を返す関数等とは異なり、累乗根全てを List として返します。　n乗根は全部で n　個あるので、返される List のサイズは引数で指定した自然数と一致します。　返される累乗根の値は ${ k = 0,\,1,\,\cdots,\,n-1 }$ として

　　 ${ \displaystyle z_k = |z|^\frac{1}{n}\left(\cos\left(\varphi + \tfrac{2\pi k}{n}\right) + i\sin\left(\varphi + \tfrac{2\pi k}{n}\right)\right) \qquad (\varphi = \arg(z)) }$