座標変換でドップラー効果の公式を導いてみる：音源が動く場合

ガリレイ変換を用いて音のドップラー効果 (Doppler effect) の公式を導いてみます（目次）。　今回は音源のみが動いて、観測者は静止している場合を考えます。

音源が静止している場合

まずは準備として、位相 ${ \theta(x,\,t) }$ が音速にどのように依存しているかを考えます。　音速を ${ V }$ とすると ${ kV = \omega }$ が成り立つので、位相 ${ \theta(x,\,t) }$ は

　　 ${ \displaystyle \begin{align*} \theta(x,\,t) &= kx - \omega t \\ &= \frac{\omega}{V}x - \omega t \end{align*} }$

となります。

音源が運動している場合

観測者 (observer) が静止していて、音源 (source) が速度*1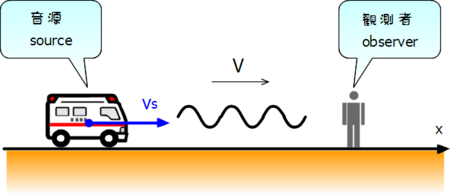 ${ v_s }$ で動いている状況を考えます。

図では右方向を ${ x }$ 軸の正の方向とし、 ${ v_s,\,V }$ を正としてます。　 ${ V }$ は音速。

音源が静止している座標系では

音源が静止している座標系では波数（波長）や角振動数は発した音のものそのままですが、音速が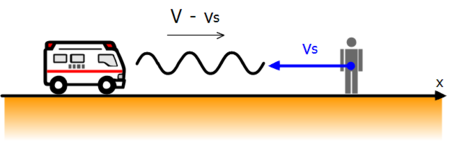 ${ V - v_s }$ のように変化します*2。

このとき ${ \theta(x,\,t) }$ は

　　 ${ \displaystyle \begin{align*} \theta(x,\,t) = \frac{\omega}{V-v_s}x - \omega t \end{align*} }$

となります。

観測者が静止している座標系へ座標変換する

次に音源が静止している座標系から、観測者が静止している座標系へ座標変換します。　観測者が静止している座標系は ' を付けて ${ (x',\,t') }$ としましょう。　変換はガリレイ変換ですが、運動している方向に注意：

　　 ${ \displaystyle \begin{align*} \begin{cases} x &\longrightarrow\quad x' = x + v_s t \\ t &\longrightarrow\quad t' = t \end{cases} \end{align*} }$

これを逆に解くと

　　 ${ \displaystyle \begin{align*} \begin{cases} x = x' - v_s t' \\ t = t' \end{cases} \end{align*} }$

となります。　よって、この変換を ${ \theta(x,\,t) }$ に施すと

　　 ${ \displaystyle \begin{align*} \theta(x,\,t) &= \frac{\omega}{V - v_s}\left(x' - v_s t' \right) - \omega t' \\ &= \frac{\omega}{V - v_s}x' - \left(1 + \frac{v_s}{V - v_s}\right)\omega t' \\ &= \frac{\omega}{V - v_s} x' - \frac{V}{V - v_s}\omega t' \end{align*} }$

これが ${ \theta'(x',\,t') = k'x' - \omega't' }$ に等しくなる（位相が共変）として

　　 ${ \displaystyle \begin{align*} k' &= \dfrac{\omega}{V - v_s} , & \omega' &= \dfrac{V}{V - v_s}\omega \end{align*} }$

を得ます。　ただし、 ${ k',\,\omega' }$ は観測者が静止している座標系での波数と角振動数、つまり観測者が観測する波数と角振動数です。

波長と振動数の変換

上記の波数と角振動数の変換式から、波長と振動数の変換式を導くと

　　 ${ \displaystyle \begin{align*} \lambda' &= \frac{2\pi}{k'} = 2\pi\frac{V - v_s}{\omega} = \frac{V - v_s}{V}\lambda = \frac{V-v_s}{V}\lambda \\ \nu' &= \frac{\omega'}{2\pi} = \frac{V}{V - v_s}\frac{\omega}{2\pi} = \frac{V}{V - v_s}\nu \end{align*} }$