以前、「倭算数理研究所」で書いていた commons-math 解読シリーズの記事ですが明らかに書くブログを間違えたので、commons-math3 が出たこの期にこちらへ移転します。
今回は org.apache.commons.math3 パッケージ内に定義されている Field, FieldElement インターフェースについて見ていきます。
Field とは日本語で「体(タイ)」と呼ばれるもので、大雑把に言えば加減乗除の演算が定義された集合です。 具体的には有理数(分数)全体の集合、実数全体の集合など(通常の加減乗除の演算と合わせて)です。 整数は割り算ができないので体ではありません。 数学での定義は後に書いたので、興味のある方はそちらをどうぞ。 1つの体に関して Field オブジェクトは1つだけしか存在しない、つまり Field インターフェースを実装している具象クラスはシングルトンであることが望ましいようです。
FieldElement は上記の Field に含まれている要素です。 1つの有理数、1つの実数それぞれが FieldElement オブジェクトになります。
commons-math には代数系として「体」しか定義されていませんが、他にも「群 (Group)」・「環 (Ring)」などもあります。 それらを使いたい方は JScience の org.jscience.mathematics.structure パッケージに定義されているクラス群を使ってみるといいかもしれません。 ただし、そこに定義されている Field は、commons-math での FieldElement に対応するものなので注意が必要です。
では、以下で Field, FieldElement の定義と実装クラスを見ていきましょう。
Field<T> インターフェース
まずは Field<T> インターフェース。 型パラメータ T はこの Field の要素の型です:package org.apache.commons.math3; public interface Field<T>{ T getZero(); T getOne(); Class<? extends FieldElement<T>> getRuntimeClass(); }
getZero(), getOne() メソッドはそれぞれ和演算 (+) と積演算 (*) の単位元を取得するメソッドです。 返り値はどちらも T になってますが、これらは後で見る FieldElement オブジェクトでないといけないはずなので、本当なら
public interface Field<T extends FieldElement<T>>{ ... }
となっているべきなんですが・・・ おそらく実装者が Generics に不慣れだったんでしょう。 もう変更不可能。 まぁ、そんなに困らないかと思いますが。 また、getRuntimeClass() メソッドはこの Field オブジェクトの要素となる FieldElement クラスの Class オブジェクトを返します。 まぁ、BigRealField オブジェクトに対して BigReal クラス、ComplexField オブジェクトに対して Complex クラスなどです。
commons-math 内に定義されている Field インターフェースの実装クラスには、以下のものがあります:
- FractionField / BigFractionField (org.apache.commons.math3.fraction パッケージ)
- BigRealField (org.apache.commons.math3.util パッケージ)
- DfpField (org.apache.commons.math3.dfp パッケージ)
- ComplexField (org.apache.commons.math3.complex パッケージ)
各クラスの詳細については後日に。
FieldElement<T> インターフェース
次は FieldElement<T> インターフェース。 実際にプログラミングで使うのはこのインターフェースを実装したクラスのオブジェクトです。package org.apache.commons.math3; public interface FieldElement<T>{ // 体 Field<T> getField(); // 逆元 T negate(); T reciprocal(); // 加減乗除 T add(T a); T subtract(T a); T multiply(T a); T multiply(int n); T divide(T a); }
この要素が属する「体」に対応する Field オブジェクトを取得するメソッド、和・積に関する逆元を返すメソッド、そして加減乗除の演算に対応するメソッドが定義されています。 この FieldElement インターフェースも、本当なら
public FieldElement<T extends FieldElement<T>>{ ... }
のように定義されるべきでしょうね。 まぁそれはともかく、commons-math3 内に定義されている FieldElement の実装クラスには
- Fraction / BigFraction
- BigReal
- Dfp / DfpDec
- Complex
などがあります。 パッケージは上記のそれぞれの体と同じです。 これらも後日に。
ちょっと数学を
代数学での「体」の定義は、以下のようになっています(x, y, z はこの体の要素とします):
- 和演算 (+) に関して
- 積演算 (*) に関して
- 和演算・積演算に関して
- 分配法則が成り立つ : x*(y+z) = x*y + x*z, (y+z)*x = y*x + z*x
これに加えて積演算に関する交換法則 x*y = y*x が成り立つものを「可換体 (commutative field)」といいます。 commons-math で定義されている「体」は全て可換体です。
では、commons-math の Field, FieldElement が上記の体の定義を満たしているのかを見ていきましょう:
- 和演算 (FieldElement#add()) に関して
- 積演算 (FieldElement#multiply()) に関して
- 和演算・積演算に関して
- 分配法則・・・実装者への制約
って感じになってます。 結合法則、交換法則、分配法則は「実装者への制約」で仕方ないと思いますが、逆元を返すメソッドは定義しておいてほしいところ commons-math3 から逆元を返すメソッドも定義されました。
余談:代数系
「体」の数学的な定義を見ましたが、ついでにいくつか代数系の定義も見ておきましょう。半群
「半群 (semi-group)」とは、ある集合に積演算 (*) が定義されていて、積演算に関して以下を満たすもの:正確には、単位元が無いものを「半群」、単位元があるものを「単位元付半群」と言うそうです。 以下では、上記の3つの条件を満たすものを「半群」とします。
群 / 可換群 / 加法群
「半群」がさらに
- 積演算に関して、各元 x に逆元 x-1 が存在する
を満たすとき、これを「群 (group)」と言います。 さらに
- 積演算に関して、交換法則が成り立つ : x*y = y*x
を満たすとき「可換群 (commutative group)」と言います。
「群」で演算を * の代わりに + と書いたものを、慣習的に「加法群 (additive group)」を言います。 通常、加法群として扱うものは「可換群」でもあります。 単位元は「1」の代わりに「0」を使います。
環 Ring
ある集合に2つの演算、和演算 (+) と積演算 (*) が定義されていて
- 和演算に関して可換群
- 積演算に関して半群
- 分配法則が成り立つ・・・ x*(y+z) = x*y + x*z, (y+z)*x = y*x + z*x
を満たすとき、この集合を「環 (ring)」と言います。 積演算に関して交換法則が成り立つ場合、これを「可換環 (commutative ring)」といいます。
体 Field
「体」の定義は上記で述べましたが、これは「0(和演算の単位元)以外の元に関して積演算が群をなす環」と言い換えることができます。 これらの代数系をクラス図にするとこんな感じ: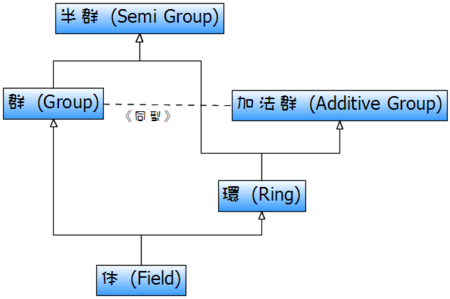
《同型》の意味はちょっとおかしいですけどあまり深く考えないでね:-p

数学ガール フェルマーの最終定理 (数学ガールシリーズ 2)
- 作者: 結城浩
- 出版社/メーカー: ソフトバンククリエイティブ
- 発売日: 2008/07/30
- メディア: ペーパーバック
- 購入: 35人 クリック: 441回
- この商品を含むブログ (260件) を見る

- 作者: 齋藤正彦
- 出版社/メーカー: 東京大学出版会
- 発売日: 2002/08
- メディア: 単行本
- クリック: 21回
- この商品を含むブログ (19件) を見る