2次元で「回転 + 平行移動 = 回転」は容易に分かる？

『統計物理学下第3版』の「第13章　結晶の対称性」を読んでいて「ん？」と思ったんだけど、3次元の結晶に関して

ある角度だけの回転とそれに続く回転軸に垂直な方向への平行移動は、容易にわかるように、最初の軸に平行な他の軸のまわりの同じ角度だけの単なる回転と等価である。

らしい。　そんなに容易にわかることかなぁ？　容易に分かるというなら等価な回転の中心がどのあたりにあるのかすぐ分かってもよさそうだけどあんまりぴんとこない。　ということでキチンと数式で確かめてやりましょう。　上記の話は3次元結晶のものですが、平面上の回転や平行移動の話なので2次元座標を扱います。

準備：同次座標

平面内での回転と平行移動をベクトルとして扱うためには、通常の2成分のベクトルではなく同次座標という3成分のベクトルを使う必要があります。　・・・正直まじめに使ったことがないので、まず簡単な確認から。　同次座標では、点 ${ (x,\,y) }$ を

　　 ${ \displaystyle \begin{align*} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{align*} }$

で表します。　第3成分は1でなくてもいいそうですが、こうしておいた方が計算がいろいろ簡単だそうで。　次に、この点を平行移動、回転させる一次変換（行列）を見ておきましょう。　まず ${ x,\,y }$ 方向にそれぞれ ${ p,\,q }$ だけ平行移動する変換行列 ${ D(p,\,q) }$ は

　　 ${ \displaystyle \begin{align*} D(p,\,q) = \begin{pmatrix} 1 & 0 & p \\ 0 & 1 & q \\ 0 & 0 & 1 \end{pmatrix} \end{align*} }$

で与えられます。　実際、

　　 ${ \displaystyle \begin{align*} D(p,\,q) \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x+p \\ y+q \\ 1 \end{pmatrix} \end{align*} }$

となります。　また、原点の周りに ${ \theta }$ だけ回転する変換行列 ${ R(\theta) }$ は

　　 ${ \displaystyle \begin{align*} R(\theta) = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{align*} }$

です。　これはほとんど平面上の2×2回転行列と同じなので説明は不要かと。

「回転＋平行移動 = 回転」の証明

では「回転の後に平行移動を施す変換は、別の1つの回転と同じになる」ことを示しましょう。

回転 + 平行移動

原点の周りに ${ \theta }$ だけ回転し、その後で ${ x,\,y }$ 方向にそれぞれ ${ p,\,q }$ だけ平行移動する変換行列は

　　 ${ \displaystyle \begin{align*} D(p,\,q)R(\theta) &= \begin{pmatrix} 1 & 0 & p \\ 0 & 1 & q \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix}\\ &= \begin{pmatrix} \cos\theta & -\sin\theta & p \\ \sin\theta & \cos\theta & q \\ 0 & 0 & 1 \end{pmatrix} \end{align*} }$

原点以外の点の周りの回転

点 ${ A(a,\,b) }$ の周りに ${ \theta }$ だけ回転する変換行列は

　　 ${ \displaystyle \begin{align*} D(a,\,b)R(\theta)D(-a,\,-b) &= \begin{pmatrix} 1 & 0 & a \\ 0 & 1 & b \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & -a \\ 0 & 1 & -b \\ 0 & 0 & 1 \end{pmatrix}\\ &= \begin{pmatrix} \cos\theta & -\sin\theta & a \\ \sin\theta & \cos\theta & b \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & -a \\ 0 & 1 & -b \\ 0 & 0 & 1 \end{pmatrix}\\ &= \begin{pmatrix} \cos\theta & -\sin\theta & -a\cos\theta+b\sin\theta+a \\ \sin\theta & \cos\theta & -a\sin\theta-b\cos\theta+b \\ 0 & 0 & 1 \end{pmatrix} \end{align*} }$

同じ変換になるためには・・・

上記の2つの変換が等価になる条件を求めましょう。　回転角は同じ値でなければならないのは、行列の左上2行2列を見れば明らか（同じ文字を使ってるので逆にややこしいかな？）。　で、もう少し条件を見ていく必要があるのは、1つの回転としたときの回転の中心がどこになるのかです。　この中心の座標 ${ A(a,\,b) }$ を回転角 ${ \theta }$ と平行移動量 ${ p,\,q }$ で表すのがミッション。　条件は変換行列 (1, 3), (2, 3) 成分を見比べるだけ。

　　 ${ \displaystyle \begin{align*} \begin{cases} p &= -a\cos\theta+b\sin\theta+a \\ q &= -a\sin\theta-b\cos\theta+b \end{cases} \qquad\cdots (1) \end{align*} }$

行列で書くと

　　 ${ \displaystyle \begin{align*} \begin{pmatrix} p \\ q \end{pmatrix} &= \begin{pmatrix} 1-\cos\theta & \sin\theta \\ -\sin\theta & 1-\cos\theta \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} \end{align*} }$

です。　これを逆に解くと（補遺参照）

　　 ${ \displaystyle \begin{align*} \begin{pmatrix} a \\ b \end{pmatrix} &= \tfrac{1}{2}\begin{pmatrix} 1 & -\cot\tfrac{\theta}{2} \\ \cot\tfrac{\theta}{2} & 1 \end{pmatrix} \begin{pmatrix} p \\ q \end{pmatrix} \end{align*} }$

つまり

　　 ${ \displaystyle \begin{align*} \begin{cases} a = \tfrac{1}{2}\left( p - q\cot\tfrac{\theta}{2} \right) \\ b = \tfrac{1}{2}\left( p\cot\tfrac{\theta}{2} + q \right) \end{cases} \qquad \cdots(2) \end{align*} }$

を得ます。

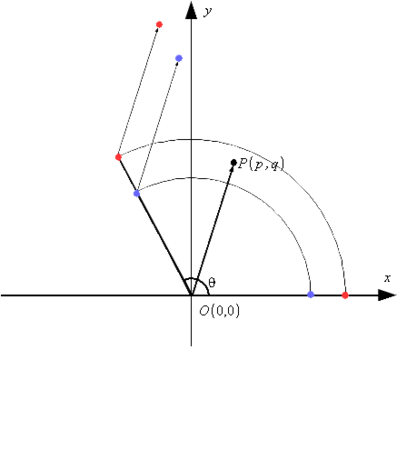
回転の中心はどこにあるのか？

平行移動する量 ${ p,\,q }$ を使って点 ${ P }$ を ${ P(p,\,q) }$ で定めましょう。　点 ${ A }$ が点 ${ P }$ に大してどんな位置にあるのかを考察してみましょう。

まず、必須の手順ではありませんが、点 ${ A }$ がどのあたりにあるかの目星。　(1) 式を以下のように変形します：

　　 ${ \displaystyle \begin{align*} \begin{cases} p-a &= -a\cos\theta+b\sin\theta \\ q-b &= -a\sin\theta-b\cos\theta \end{cases} \end{align*} }$

この各辺を自乗し、辺々を加えると

　　 ${ \displaystyle \begin{align*} (p-a)^2 + (q-b)^2 = a^2 + b^2 \end{align*} }$

を得ます。これは点 ${ A }$ が原点 ${ O }$ と点 ${ P }$ から等距離にある、すなわち点 ${ A }$ は線分 ${ OP }$ の垂直二等分線上にあるということが分かります。

では、もう少し点 ${ A }$ のきちんとした位置を求めておきましょう。　(2) 式の両辺を自乗して辺々を加えると

　　 ${ \displaystyle \begin{align*} a^2 + b^2 = \tfrac{1}{4}\left(1+\cot^2\tfrac{\theta}{2}\right)\left(p^2 + q^2\right) \end{align*} }$

ここで公式（「三角関数の公式を復習する (1) ：三角関数の定義と相互関係」など参照）

　　 ${ \displaystyle \begin{align*} 1 + \cot^2\theta = \frac{1}{\sin^2\theta} \end{align*} }$

を使うと

　　 ${ \displaystyle \begin{align*} & a^2 + b^2 = \frac{1}{4\sin^2\frac{\theta}{2}}\left(p^2 + q^2\right) \\ \therefore & \tfrac{1}{2}OP = OA \sin\tfrac{\theta}{2} \end{align*} }$

これを図形的に見ると、線分 ${ OP }$ の中点を ${ M }$ として、「点 ${ A }$ は ${ \angle OAM }$ が ${ \tfrac{\theta}{2} }$ と位置にある」ことが分かります。　また、 ${ \angle OMA = \tfrac{\pi}{2} (= 90^\circ) }$ であることを使うと

点 ${ A }$ は ${ \angle P O A = \tfrac{\pi-\theta}{2} }$ の位置にある

となります。　まぁ、文章で説明してもわかりにくいので図示してみましょう：

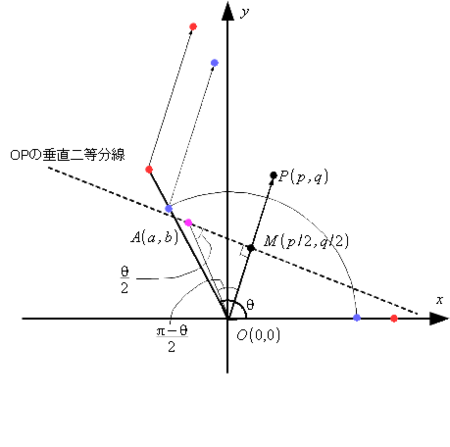
だいたいどんな位置に点 ${ A }$ があるか分かったでしょうか？

これでランダウ・リフシッツに載ってた主張は証明完了（細部に目を瞑れば）。　最初この主張で「ん？」と思ったのは、不動点（変更の前後で位置が変わらない）がある回転と不動点がない平行移動を合わせて不動点がある回転と等価になる、というのがちょっと不思議に思ったからと言うのがあるんですが、これは回転によって丁度その後の平行移動と逆に平行移動される点があって、それらが打ち消しあうことによって不動点が生じるということのようでした。　これが等価な回転の中心になるのね。　ふむふむ。

補遺

行列 ${ \Theta(\theta) }$ を

　　 ${ \displaystyle \begin{align*} \Theta(\theta) = \begin{pmatrix} 1-\cos\theta & \sin\theta \\ -\sin\theta & 1-\cos\theta \end{pmatrix} \end{align*} }$

で定義します。　この行列の逆行列を求めれば OK。　まず行列式は

　　 ${ \displaystyle \begin{align*} \left|\Theta(\theta)\right| &= \begin{vmatrix} 1-\cos\theta & \sin\theta \\ -\sin\theta & 1-\cos\theta \end{vmatrix} \\ &= (1-\cos\theta)^2 + \sin^2\theta \\ &= 2(1 - \cos\theta) \end{align*} }$

よって逆行列は

　　 ${ \displaystyle \begin{align*} \Theta^{-1}(\theta) &= \frac{1}{2(1-\cos\theta)}\begin{pmatrix} 1-\cos\theta & -\sin\theta \\ \sin\theta & 1-\cos\theta \end{pmatrix} \\ &= \tfrac{1}{2}\begin{pmatrix} 1 & -\frac{\sin\theta}{1-\cos\theta} \\ \frac{\sin\theta}{1-\cos\theta} & 1 \end{pmatrix} \\ &= \tfrac{1}{2}\begin{pmatrix} 1 & -\frac{2\sin\tfrac{\theta}{2}\cos\tfrac{\theta}{2}}{2\sin^2\tfrac{\theta}{2}} \\ \frac{2\sin\tfrac{\theta}{2}\cos\tfrac{\theta}{2}}{2\sin^2\tfrac{\theta}{2}} & 1 \end{pmatrix} \\ &= \tfrac{1}{2}\begin{pmatrix} 1 & -\cot\tfrac{\theta}{2} \\ \cot\tfrac{\theta}{2} & 1 \end{pmatrix} \end{align*} }$