正四面体の計量 - 倭算数理研究所

目的は正十二面体、正二十面体の体積を求めることなんですが、ちょっと準備運動として正四面体、正六面体（立方体）、正八面体の体積等を求めていきす。

幾何学的対象の個数等
隣り合う2つの面のなす角
表面積
体積
内接球・辺に接する球・外接球の半径

一辺の長さを ${ a }$ とし、以下のように頂点に名前を付けておきます。

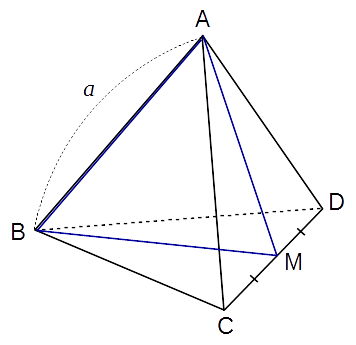
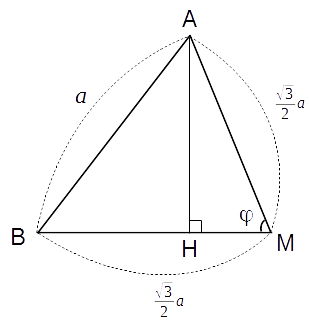
M は辺CD の中点です。　AM, BM の長さは

　　 $\textrm{AM} = \textrm{BM} = a \sin \frac{\pi}{3} = \frac{\sqrt{3}}{2}a$

です。　 ${ \varphi }$ は隣り合う2つの面のなす角で、後で求めます。

幾何学的対象の個数等

面の数 ${ f }$	4
辺の数 ${ e }$	6
頂点の数 ${ v }$	4
面の形状（正 ${ m }$ 角形）	正三角形 ( ${ m = 3 }$ )
1つの頂点に集まる面の個数 ${ p }$	3
双対パートナー	正四面体（自己双対）

オイラーの関係式は

　　 $f - e + v = 4 - 6 + 4 = 2$

となって確かに成り立ってますね。

正多面体で面の数 ${ f }$ 、面の形状（正 ${ m }$ 角形）、1つの頂点に集まる面の個数 ${ p }$ が分かっているとき、辺の数 ${ e }$ と頂点の数 ${ v }$ は（簡単な組み合わせの計算から）

　　 $e = \frac{mf}{2},\qquad v = \frac{mf}{p}$

で与えられます。　今の場合に実際に確かめてみると

　　 ${ \displaystyle \begin{align*} e &= \frac{3 \cdot 4}{2} = 6 \\ v &= \frac{3 \cdot 4}{3} = 4 \end{align*} }$

となり、成り立っています。

隣り合う2つの面のなす角 ${ \varphi }$

△ABM に余弦定理を適用して

　　 ${ \displaystyle \begin{align*} \cos \varphi &= \frac{\left(\frac{\sqrt{3}}{2}a\right)^2 + \left(\frac{\sqrt{3}}{2}a\right)^2 - a^2}{2\cdot \frac{\sqrt{3}}{2}a \cdot \frac{\sqrt{3}}{2}a} = \frac{\frac{1}{2}a^2}{\frac{3}{2}a^2} \\ &= \frac{1}{3} \end{align*} }$

これは約70°です。

表面積 ${ S }$

「正多角形の面積」で正三角形の面積を辺の長さで表した表式を導きました。　正四面体の面の個数はもちろん4なので、正四面体の面積は
　　 ${ \displaystyle \begin{align*} S &= 4\cdot \frac{\sqrt{3}}{4}a^2 \\[2mm] &= \sqrt{3} a^2 \end{align*} }$

体積 ${ V }$

頂点 A から △BCD に下ろした垂線の足を H とします。　△BCD を底面と見たとき、線分 AH がこの正四面体の高さとなります。

H が△BCD の重心であること

△ABH, △ACH, △ADH が合同なので（証明略）、 ${ \textrm{BH} = \textrm{CH} = \textrm{DH} }$ 。　よって H は △BCD の外心となる。　正三角形の外心と重心は一致するので、H は △BCD の重心である。

BH の長さ

BM が△BCD の中線*1であり、H が △BCD の重心であることから、H は線分 BM 上にあり、 ${ \textrm{BH} : \textrm{HM} = 2 : 1 }$ が成り立つ（証明略）。　よって

　　 ${ \displaystyle \begin{align*} \textrm{BH} &= \frac{2}{3} \textrm{BM} \\ &= \frac{\sqrt{3}}{3}a \end{align*} }$

AH の長さ

直角三角形 ABH に三平方の定理を用いると

　　 ${ \displaystyle \begin{align*} \textrm{AH} &= \sqrt{a^2 - \left(\frac{\sqrt{3}}{3}a\right)^2} = \sqrt{\frac{2}{3}}a \\[2mm] &= \frac{\sqrt{6}}{3}a \end{align*} }$

正四面体の体積

△BCD の面積は ${ \frac{\sqrt{3}}{4}a^2 }$ なので、正四面体の体積 ${ V }$ は

　　 ${ \displaystyle \begin{align*} V &= \frac{1}{3} \cdot \frac{\sqrt{3}}{4}a^2 \cdot \frac{\sqrt{6}}{3}a \\ &= \frac{\sqrt{2}}{12}a^3 \end{align*} }$

となります。

内接球・辺に接する球・外接球の半径 ${ r,\,\rho,\,R }$

体積を求めるのが一応の目的で、それは達成できたのですが、ついでにいくつかの球に関して半径を求めておきましょう。　正多面体の場合は内接円、外接円の半径を求めましたが、ここでも同じような球に対して半径を求めておきましょう。　求めるのは

内接球（各面に接する球）の半径 ${ r }$
辺に接する球の半径 ${ \rho }$
外接球（各頂点を通る球）の半径 ${ R }$

「辺に接する球」って名前がありそうだけど知らないので長い名前で書いてます。

内接球・外接球の半径 ${ r,\,R }$

さて、では各半径の長さを求めていきましょう。　まずは 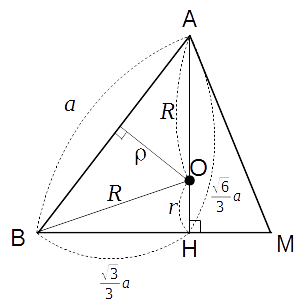${ r,\,R }$ をいっしょに求めます。　体積を求める際に用いた △ABM の断面にもう少し補助線を引くと（ここには ${ \rho }$ も書き入れてます）
f:id:waman:20150922115611p:plain

上図より

　　 $R + r = \frac{\sqrt{6}}{3}a \qquad\cdots(1)$

が分かります。　また、直角三角形 OBH に注目して

　　 ${ \displaystyle \begin{align*} r^2 + \left(\frac{\sqrt{3}}{3}a\right)^2 &= R^2 \\ r^2 + \frac{1}{3}a^2 &= R^2 \qquad\cdots(2) \end{align*} }$

(1) を ${ R }$ について解いて (2) に代入すると

　　 ${ \displaystyle \begin{align*} r^2 + \frac{1}{3}a^2 &= \left(\frac{\sqrt{6}}{3}a - r\right)^2 \\ r^2 + \frac{1}{3}a^2 &= \frac{2}{3}a^2 - \frac{2\sqrt{6}}{3}ar + r^2 \\ \frac{2\sqrt{6}}{3}r &= \frac{1}{3}a \\ r &= \frac{\sqrt{6}}{12}a \end{align*} }$

となり ${ r }$ が求まりました。　これを (1) に代入して

　　 ${ \displaystyle \begin{align*} R &= \frac{\sqrt{6}}{3}a - \frac{\sqrt{6}}{12}a \\ &= \frac{\sqrt{6}}{4}a \end{align*} }$

となります。　ちなみに

　　 $r : R = 1 : 3$

となり、 ${ \textrm{AO} : \textrm{OH} = 3 : 1 }$ が成り立っています。

体積から内接円の半径を求める

上記の導出とは別に体積から内接球の半径を求めてみましょう。　正四面体 ABCD は、重心 O を頂点とし正三角形の各面を底面とする4つの合同な三角錐に分割できます。　このとき、各三角錐の高さが内接球の半径 ${ r }$ になるので、正四面体の体積 ${ V = \frac{\sqrt{2}}{12}a^3 }$ 、面の個数 ${ f = 4 }$ 、面の面積 ${ s = \frac{\sqrt{3}}{4}a^2 }$ の間には以下が成り立ちます：

　　 $V = f \cdot \frac{1}{3} r s$

これから ${ r }$ を求めると

　　 ${ \displaystyle \begin{align*} \frac{\sqrt{2}}{12}a^3 &= 4 \cdot \frac{1}{3} r \cdot \frac{\sqrt{3}}{4}a^2 \\ r &= \frac{\sqrt{6}}{12}a \end{align*} }$

となって、先ほどの結果と一致します。

辺に接する球の半径 ${ \rho }$

上図で長さ ${ \rho }$ の線分を含む直角三角形に対して三平方の定理を用いると

　　 ${ \displaystyle \begin{align*} \rho &= \sqrt{R^2 - \left(\frac{1}{2}a\right)^2} = \sqrt{\frac{3}{8}a^2 - \frac{1}{4}a^2} = \sqrt{\frac{1}{8}a^2} \\ &= \frac{\sqrt{2}}{4}a \end{align*} }$

を得ます。

${ r,\,\rho,\,R }$ の比

上記で求めた3つの半径の比を求めてみると

　　 ${ \displaystyle \begin{align*} r : \rho : R &= \frac{\sqrt{6}}{12}a : \frac{\sqrt{2}}{4}a : \frac{\sqrt{6}}{4}a \\ &= 1 : \sqrt{3} : 3 \end{align*} }$