正八面体の計量 - 倭算数理研究所

今回は正八面体の表面積、体積等を求めていきす。　このあたりまでは高校レベルの数学で解けますね。　導出の都合上、今までと求める量の順番を変えてます。

幾何学的対象の個数等
内接球・辺に接する球・外接球の半径
表面積
体積
隣り合う2つの面のなす角

一辺の長さを ${ a }$ とし、以下のように頂点に名前を付けておきます。

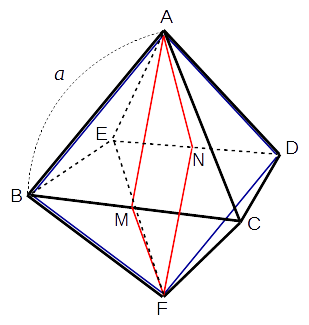
この正八面体を青い線、赤い線に沿って切ると、それぞれ以下のような断面が得られます（青 → 左、赤 → 右）：
f:id:waman:20150923074907p:plain

${ \varphi }$ は隣り合う2つの面のなす角です。

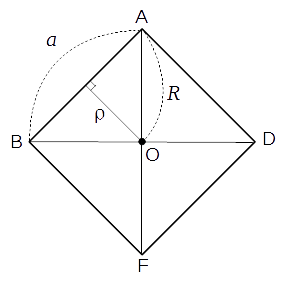
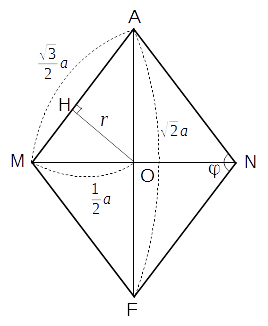
幾何学的対象の個数等

面の数 ${ f }$	8
辺の数 ${ e }$	12
頂点の数 ${ v }$	6
面の形状（正 ${ m }$ 角形）	正三角形 ( ${ m = 3 }$ )
1つの頂点に集まる面の個数 ${ p }$	4
双対パートナー	正六面体（立方体）

オイラーの関係式は

　　 $f - e + v = 8 - 12 + 6 = 2$

となって成り立ってます。

正多面体で面の数 ${ f }$ 、面の形状（正 ${ m }$ 角形）、1つの頂点に集まる面の個数 ${ p }$ から辺の数 ${ e }$ と頂点の数 ${ v }$ を計算すると

　　 ${ \displaystyle \begin{align*} e &= \frac{mf}{2} = \frac{3 \cdot 8}{2} = 12 \\ v &= \frac{mf}{p} = \frac{3 \cdot 8}{4} = 6 \end{align*} }$

となり、こちらも成り立っています。

内接球・辺に接する球・外接球の半径 ${ r,\,\rho,\,R }$

辺に接する球の半径 ${ \rho }$ と外接球の半径 ${ R }$ は、四角形ABFDが正方形（断面図左参照）であることから簡単に求まって

　　 ${ \displaystyle \begin{align*} \rho &= \frac{1}{2}a \\ R &= \frac{\sqrt{2}}{2}a \end{align*} }$

次に内接球の半径 ${ r }$ を求めましょう。　正八面体の重心 O から △ABC に下ろした垂線の足を H とすると、これは △ABC の重心となるので*1

　　 $\textrm{MH} = \frac{1}{3}\textrm{AM} = \frac{\sqrt{3}}{6}a$

ここで直角三角形OBH （断面右図参照）に注目して、三平方の定理より

　　 ${ \displaystyle \begin{align*} r^2 + \left(\tfrac{\sqrt{3}}{6}a\right)^2 &= \left(\tfrac{1}{2}a\right)^2 \\ r^2 &= \frac{1}{6}a^2 \\ r &= \frac{\sqrt{6}}{6}a \end{align*} }$

を得ます。

3つの半径の比も計算しておきましょう。

　　 ${ \displaystyle \begin{align*} r : \rho : R &= \frac{\sqrt{6}}{6}a : \frac{1}{2}a : \frac{\sqrt{2}}{2}a \\[2mm] &= \sqrt{2} : \sqrt{3} : \sqrt{6} \end{align*} }$

まぁ、それなりにキレイにまとまりましたね。

表面積 ${ S }$

表面積は、一辺の長さが ${ a }$ の正三角形8枚分なので簡単に計算できて

　　 ${ \displaystyle \begin{align*} S &= 8\cdot \frac{\sqrt{3}}{4}a^2 \\[2mm] &= 2\sqrt{3} a^2 \end{align*} }$

体積 ${ V }$

正四面体 ABCDEF は、4点 BCDE を含む平面で切ると2つの合同な正四角錐に分けられます。　これらの体積は簡単に計算できて、高さが ${ \textrm{OA} = R = \frac{\sqrt{2}}{2}a }$ であるから

　　 ${ \displaystyle \begin{align*} V &= 2 \cdot \frac{1}{3}a^2 \cdot \frac{\sqrt{2}}{2}a \\ &= \frac{\sqrt{2}}{3}a^3 \end{align*} }$

となります。

体積から内接円の半径を求める

例によって、体積 ${ V }$ から内接球の半径 ${ r }$ を求めてみましょう。

　　 ${ \displaystyle \begin{align*} \frac{\sqrt{2}}{3}a^3 &= 8 \cdot \frac{1}{3} r \cdot \frac{\sqrt{3}}{4}a^2 \\ r &= \frac{\sqrt{6}}{6}a \end{align*} }$

となって、先ほどの結果と一致します。

隣り合う2つの面のなす角 ${ \varphi }$

四角形 AMFN （断面右図）に注目して

　　 ${ \displaystyle \begin{align*} \cos \varphi &= \frac{\left(\frac{\sqrt{3}}{2}a\right)^2 + \left(\frac{\sqrt{3}}{2}a\right)^2 - 2a^2}{2\cdot \frac{\sqrt{3}}{2}a \cdot \frac{\sqrt{3}}{2}a} = -\frac{\frac{1}{2}a^2}{\frac{3}{2}a^2} \\ &= -\frac{1}{3} \end{align*} }$