正接関数 tan x の高階導関数

Twitter の TL 上に ${ \tan x }$ をどんどん微分していくツイートが流れてたのだが、こんな感じにやればいいんじゃないかという方法があるので書いてみます。

準備

${ \tan x }$ の微分は高校数学でやりますね（数学IIIなのでやらない人もいるかな）。

　　 ${ \displaystyle\begin{align*} (\tan x)' = \frac{1}{\cos^2 x} \end{align*}}$

また、後で使うこんな公式も数学Iでやりますね。

　　 ${ \displaystyle\begin{align*} 1+\tan^2 x = \frac{1}{\cos^2 x} \end{align*}}$

小さい ${ n }$ について実行してみる

さて、上記の公式を踏まえて、実際に ${ \tan x }$ の微分を計算してみましょう。　合成関数の微分を使ってるので、数学III前提ですが。　結果を ${ \tan x }$ のみで表すのがミソですかね。

　　 ${ \displaystyle\begin{align*} (\tan x)' &= \frac{1}{\cos^2 x} \\ &= 1 + \tan^2 x \end{align*}}$

　　 ${ \displaystyle\begin{align*} (\tan x)'' &= (1+\tan^2 x)' \\ &= 2\tan x \cdot \frac{1}{\cos^2 x} \\ &= 2\tan x (1+\tan^2 x) \\ &= 2\tan x + 2\tan^3 x \end{align*}}$

　　 ${ \displaystyle\begin{align*} (\tan x)''' &= (2\tan x + 2\tan^3 x)' \\ &= (2 + 6\tan^2 x) \frac{1}{\cos^2 x} \\ &= (2 + 6\tan^2 x) (1+\tan^2 x) \\ &= 2 + 8\tan^2 x + 6\tan^4 x \end{align*}}$

　　 ${ \displaystyle\begin{align*} (\tan\theta)'''' &= (2 + 8\tan^2 x + 6\tan^4 x)' \\ &= (16\tan x + 24\tan^3 x) (1+\tan^2 x) \\ &= 16\tan x + 40\tan^3 x + 24\tan^5 x \end{align*}}$

ちょっと途中式を書きすぎてゴチャゴチャしてしまってますが、結果だけ書くと以下のようになります：

　　 ${ \displaystyle\begin{align*} \begin{matrix} \tan x =& & \tan\theta \\ (\tan x)' =& 1&& + \tan^2 x \\ (\tan x)'' =& &2\tan x && + 2\tan^3 x \\ (\tan x)''' =& 2&& + 8\tan^2 x && + 6\tan^4 x \\ (\tan x)'''' =& &16\tan x && + 40\tan^3 x && + 24\tan^5 x \end{matrix} \end{align*}}$

${ \tan x }$ の ${ n }$ 階導関数は、 ${ \tan x }$ の ${ n+1 }$ 次式で、 ${ n+1 }$ と同じ偶奇を持つ次数の項しか出てこないようですね。

係数を表を使って計算する

上記の具体的に微分を実行する方法を眺めると、 ${ \tan x }$ の ${ n }$ 階の導関数を得るには、

${ \tan x }$ の ${ n-1 }$ 階の導関数を ${ \tan x }$ で微分する
${ (1+\tan^2 x) }$ を掛ける

という手順を繰り返せばいいだけだと分かります。　 ${ 1+\tan^2 x }$ を掛けた後に展開して同類項をまとめるのは、二項係数をパスカルの三角形を使って計算するのと似たことをすればいいので、下図のように係数だけを抜き出して算数っぽく計算していくことができます。

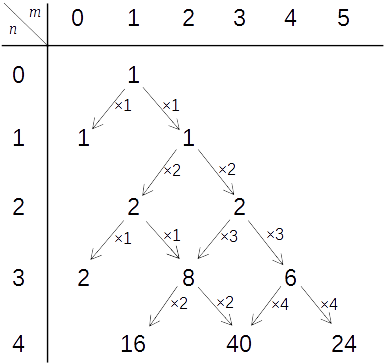
各マスの数字は、 ${ \tan x }$ の ${ n }$ 階の導関数の ${ \tan^m x }$ の係数となっています（数字がないところは0）。　あるマスの数字を計算するには、左上の数字と右上の数字を見て、それぞれの数字に ${ m }$ の値を掛けて足し算をします。　2つの数字で掛ける ${ m }$ の値が違うので注意。 ${ m }$ の数字を掛けるのがパスカルの三角形と違うところですね。

この手順を繰り返すと

n \ m	0	1	2	3	4	5	6	7	8
0		1
1	1		1
2		2		2
3	2		8		6
4		16		40		24
5	16		136		240		120
6		272		1232		1680		720
7	272		3968		12096		13440		5040
8		7936		...
9	7936		...

のような表ができますが、これから

　　 ${ \displaystyle\begin{align*} (\tan x)^{(7)} = 272 + 3968\tan^2 x + 12096\tan^4 x + 13440 \tan^6 x + 5040 \tan^8 x \end{align*}}$

だとか、 ${ (\tan x)^{(9)} }$ の定数項が 7936 であることなどが分かります。

もう少し数式を使って真面目に解く（一部だけど）方法は『続・正接関数 tan x の高階導関数』参照。

【補足1】

${ m=0 }$ の左端の列の数字を ${ n! }$ で割ると、 ${ \tan x }$ の冪展開（テイラー展開）の係数が得られます（ ${ \tan x }$ の冪展開に関しては、昔に記事書いた）。　 ${ \tan x }$ の展開にはベルヌーイ数が出てきますが、 ${ \tan x }$ の高階導関数の係数ってベルヌーイ数使って書けそうだけどどうなんでしょ？*1。