指数関数の冪級数から指数法則を導く

以前の記事で、オイラーの公式を使って三角関数の加法定理を導きましたが、その導出では指数関数の性質として指数法則の1つ

　　 ${ \displaystyle \begin{align*} e^{x+y} = e^x e^y \end{align*} }$

を使っていました。　ただし、引数が複素数（純虚数）の場合にそれが成り立つのは自明ではありません。　この記事では実際にそれが成り立つことを証明しましょう。　この証明自体は理系学部なら1, 2回生くらいで学ぶくらいの内容です。

確認

まずは次の2点を復習。

指数関数の冪級数による定義
二項定理

指数関数の冪級数による定義

指数関数の冪級数。

　　 ${ \displaystyle \begin{align*} e^x = \sum_{n=0}^\infty \frac{x^n}{n!} \end{align*} }$

引数が実数の場合は、これは冪級数展開（テイラー展開）ですが、引数が複素数の場合はこれが指数関数の定義になります。　特にオイラーの公式に出てくる指数関数は引数が複素数（純虚数）なので、これが定義になりますね。

二項定理

二項定理は通常組合せ ${ {}_nC_p = \binom{n}{r} = \frac{n!}{(n-p)!p!} }$ を使って書きますが（1行目）、ここでの証明では階乗を使った形を使います：

　　 ${ \displaystyle \begin{align*} (x + y)^n &= \sum_{r=0}^n \,_nC_r x^{n-r}y^r \\ &= \sum_{p+q = n}\frac{n!}{p!\;q!}x^py^q \end{align*} }$

証明

では証明。　まずは ${ e^{x+y} }$ を定義に従って級数に書き換えていきます：

　　 ${ \displaystyle \begin{align*} e^{x+y} &= \sum_{n=0}^\infty\frac{(x + y)^n}{n!} \\ &= \sum_{n=0}^\infty\frac{1}{n!} \sum_{p+q = n}\frac{n!}{p!\;q!}x^py^q \\ &= \sum_{n=0}^\infty \sum_{p+q = n}\frac{x^p}{p!}\frac{y^q}{q!} \end{align*} }$

2つ目の ${ \sum }$ の和の範囲は「 ${ p + q = n }$ を満たす自然数 *1 ${ p,\,q }$ 全て」です。　さて、ここで二重和について和をとる順序を以下のように変更しましょう：

　　 ${ \displaystyle \begin{align*} \sum_{n=0}^\infty\sum_{p+q=n} \longrightarrow \sum_{p=0}^\infty\sum_{q=0}^\infty \end{align*} }$

この和の変更でやってることは、下図で青の線に沿った和から赤の線に沿った和に変えてるだけです：

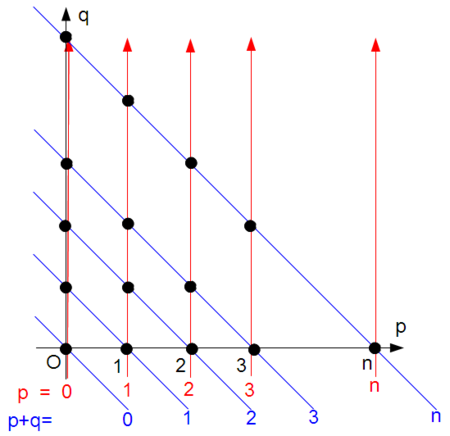
すると以下のように変形できて

　　 ${ \displaystyle \begin{align*} \sum_{n=0}^\infty \sum_{p+q = n}\frac{x^p}{p!}\frac{y^q}{q!} &= \sum_{p=0}^\infty\sum_{q=0}^\infty \frac{x^p}{p!}\frac{y^q}{q!} \\ &= \sum_{p=0}^\infty\frac{x^p}{p!} \sum_{q=0}^\infty\frac{y^q}{q!} \\[2mm] &= e^x e^y \end{align*} }$