今回から何回かにわたって org.apache.commons.math.special に定義されているクラスを見ていきます。 このパッケージにはいくつかの特殊関数 (special functions) が定義されています。 具体的には
- 誤差関数 (error function) 関連
- ガンマ関数 (gamma function) 関連
- ベータ関数 (beta function) 関連
の関数です。 今回は誤差関数関連の関数について見ていきます。
誤差関数 Error Function
誤差関数を表すクラスは Erf で、誤差関数の値を返す static メソッドなどが定義されています:package org.apache.commons.math.special; public class Erf{ public static double erf(double x){...} public static double erfc(double x){...} }
- erf() は誤差関数の値を返す
- erfc() は相補誤差関数 (complementary error function) の値を返す
それぞれの定義については以下参照。
誤差関数 erf(x)
誤差関数 erf(x) は以下のように定義されています(wikipedia:誤差関数):
に注意すると
となることが分かります(複号同順)
相補誤差関数 erfc(x)
相補誤差関数
が成り立つことが分かります。
グラフ
関数はやはりグラフを描くのがいちばんだと思うので、Groovy と JFreeChart を使って以下のようにグラフを描いてみました:@Grab('org.apache.commons:commons-math:2.2') @Grab('jfree:jfreechart:1.0.12') import org.apache.commons.math.special.Erf import org.jfree.chart.* import static org.jfree.chart.plot.PlotOrientation.VERTICAL import org.jfree.data.function.Function2D import org.jfree.data.general.DatasetUtilities def erf = { double x -> Erf.erf(x)} as Function2D def dataset = DatasetUtilities.sampleFunction2D(erf, 0d, 3d, 1000, 'erf') def chart = ChartFactory.createXYLineChart( 'Error Function', 'x', 'y', dataset, VERTICAL, true, true, true) ChartUtilities.saveChartAsPNG(new File('erf.png'), chart, 600, 400)
このスクリプトは誤差関数のみしか描画しませんが、相補誤差関数も一緒に描画すると以下のようになります:
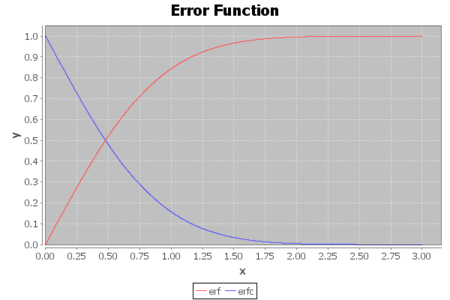
定義域 [0, 3]
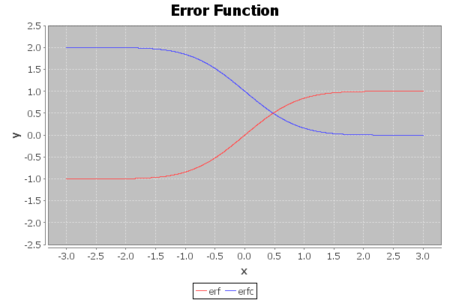
定義域 [-3, 3]
誤差関数と相補誤差関数は、直線

- 作者: 森口繁一,一松信,宇田川〓久
- 出版社/メーカー: 岩波書店
- 発売日: 1987/03/13
- メディア: 単行本
- クリック: 3回
- この商品を含むブログ (10件) を見る