今回は、前回に続き計算精度の問題をやっていきます。 対象とする物理系はガラッと変わって RC 回路になります。 といっても、この系が従う法則もニュートンの冷却の法則と同じ形の微分方程式なので、結局やってることは変わりません。
問題
d. 微分方程式
を考える。 ただし
で
とする。 この方程式は加えられた電圧が V の時の RC 回路のコンデンサーの充電過程を表す。
については秒を単位にとり、
として、この微分方程式をオイラー法で解くプログラムを書け。 t = 0.005s では3桁の精度を得るには Δt の値をどうとる必要があるか。
e. Δt = 0.005, 0.0025, 0.001 としたときの t = 0.005s における RC 回路の数値解の性質を調べよ。
RC 回路の解析解はこちらで求めてます。 結果は( のとき
の初期条件のもとで)
となります。
d.
では RC 回路のシミュレーション。 と言っても、やってることは問題 2.3 c と同じです。 物理系のドメイン分析だけやっておきましょう:- 状態変数
- 経過時間
[s] : t (BigDecimal)
- コンデンサーに充電されている電荷
[C] : q (double)
- 経過時間
- パラメータ
- 時間間隔
[s] : dt (BigDecimal)
- 電圧
[V] : v (double)
- 抵抗
: r (double)
- 静電容量
[F] : c (double)
- 時間間隔
これを踏まえて、シミュレーション・スクリプトは以下のようになります:
@GrabResolver('https://github.com/waman/groops-core/tree/master/repo') @Grab('org.waman.groops:groops-core:0.1-beta') import org.waman.groops.builder.SimulationBuilder import org.waman.groops.simulation.system.* def dtList = [5.0E-4, 2.5E-4, 1.0E-4, 5.0E-5, 2.5E-5, 1.0E-5, 0.5E-5] def tmax = 5.0E-3 new SimulationBuilder().parallel{ for(dt in dtList){ simulation{ system(new RCCircuitSystem(), dt:dt, r:2000d, c:1E-6d, v:10d) init(t:0.0, q:0d) parameterObservableSet() continueWhile{ it.t <= tmax } console(dataEntries:['dt', 'q'], outputTiming:FINAL) } } }.simulate() class RCCircuitSystem extends AnnotationObservableSystem{ @State BigDecimal t @State double q @Parameter BigDecimal dt @Parameter double v, r, c @Override void evolve(Map params){ double change = (v - q/c)/r q += change * dt.doubleValue() t += dt } }
シミュレーション結果は下表のようになります:
| dt | t = 0.005s における結果 |
|---|---|
| 0.0005 | 9.577648639678956E-6 |
| 0.00025 | 9.39442336072811E-6 |
| 0.0001 | 9.269022734871224E-6 |
| 0.00005 | 9.22470642384714E-6 |
| 0.000025 | 9.20208254807407E-6 |
| 0.00001 | 9.188359978669231E-6 |
| 0.000005 | 9.183761147410228E-6 |
よって、3桁の精度を得るには dt = 0.000005 以下にとる必要があります。
e.
こちらは問題 2.3 b と同じような問題です。 上記のシミュレーションと同じような箇所(import 文、RCCircuitSystem クラスの定義)は省略して、シミュレーション・コードは以下のようになります:double r = 2000d, c = 1E-6d, v = 10d def tmax = 5.0E-3 def analyticSolution = { BigDecimal t -> c*v*(1d - Math.exp(-t.doubleValue()/(r*c)))} double analyticQ = analyticSolution(tmax) def dtList = [5.0E-4, 2.5E-4, 1.0E-4] new SimulationBuilder().parallel{ def pngout = png(fileName:'problem2_3e.png', overwrite:true, outputTiming:FINAL){ chart(title:'problem 2.3 e', rangeLabel:'Q', range:[0.9E-5d, 1.0E-5d]){ point(label:'Simulation', x:'dt', y:'q') marker(label:'Analytic', y:analyticQ, color:java.awt.Color.BLUE) } } for(dt in dtList){ simulation{ system(new RCCircuitSystem(), dt:dt, r:r, c:c, v:v) init(t:0.0, q:0d) parameterObservableSet() continueWhile{ it.t <= tmax } dataOutputter(pngout['Simulation']) } } }.simulate()
結果は以下のようになります:
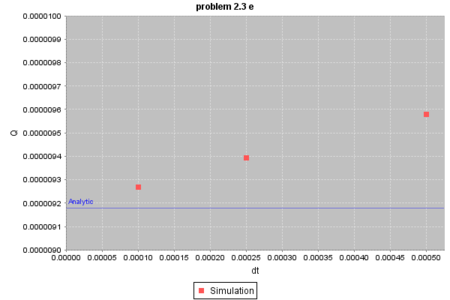
やっぱりオイラー法は1次の計算法のようですね。

- 作者: ハーベイゴールド,ジャントボチニク,Harvey Gould,Jan Tobochnik,鈴木増雄,石川正勝,溜渕継博,宮島佐介
- 出版社/メーカー: ピアソンエデュケーション
- 発売日: 2000/12
- メディア: 単行本
- 購入: 1人 クリック: 28回
- この商品を含むブログ (45件) を見る

- 作者: 関谷和愛,上原潤二,須江信洋,中野靖治
- 出版社/メーカー: 技術評論社
- 発売日: 2011/07/06
- メディア: 単行本(ソフトカバー)
- 購入: 6人 クリック: 392回
- この商品を含むブログ (155件) を見る