今回は放射性崩壊をする原子核のシミュレーション。 単一核種の場合は、ニュートンの冷却の法則にしたがう系や RC 回路と同じ形の微分方程式になるので、今までのシミュレーションと同じように行うことができます。 単一核種での放射性崩壊の法則はこちらを参照。 解析解も導いています。
問題
a. プログラム cool を修正し、原子核崩壊で使われる表記に直せ。 そして、
について、
と
のときの
の解析解の値とオイラー法の差を計算せよ。 さらに、それぞれの
の値では、その差が
に比例することを示せ。
b. 放射性崩壊の割合は、
ではなく半減期
程度の大きさを単位として与えると都合がよい。 半減期は最初の原子核の半数が崩壊する時間であり、
で与えられる。 修正したプログラムでこの関係を確かめよ。
の半減期が 4.5 × 109 年なら崩壊定数はいくらか。
c. 半減期を単位として時間を測るようにプログラムを書き換えよ。 そのプログラムで 100μg の238U が最初の量の20%に減少する時間を求めよ。
d. プログラムを2次のアルゴリズムに書き換えて、設問 a と c をもう一度行え。
今回は問題 a. のみを行います。 問題としては得に難しくなく、以前にやったcool プログラムを書き換える問題ですが、書き換えのついでにシーケンス・シミュレーション (sequence simulation) のサンプル・コードを見ていきたいと思います。
シミュレーション・スクリプト
1. まずはそのまま書き換え
最初は普通に cool シミュレーションを放射性核の場合に書き換えてみましょう。 cool プログラムに対して- 温度
→ 核の個数
- 冷却定数
→ 崩壊定数
という置き換えをするだけです。 ちなみに、核の個数 は初期値を1とした相対値を double 型として扱います:
@GrabResolver('https://github.com/waman/groops-core/tree/master/repo') @Grab('org.waman.groops:groops-core:0.2-beta') import org.waman.groops.builder.SimulationBuilder import org.waman.groops.simulation.system.* new SimulationBuilder().simulation{ system(new RadioactiveDecaySystem(), dt:0.1, lambda:1.0d) init(t:0.0, N:1.0d) continueWhile{ it.t <= 1.0 } console(outputTiming:OBSERVE_FINAL) }.simulate() class RadioactiveDecaySystem extends AnnotationObservableSystem{ @State BigDecimal t @State double N @Parameter BigDecimal dt @Parameter double lambda @Override void evolve(Map<String, Object> params) { N -= lambda * N * dt.doubleValue() t += dt } }
- problem2_7a.groovy

- 状態更新はオイラー法です。
- 反復条件は時間 t が1以下の間です。 時間 t と時間間隔 dt は BigDecimal 型にしているので、<= で評価しています。
- データ出力はとりあえず標準出力への書き出しだけです。 出力するタイミングは「OBSERVE_FINAL」としていますが、これは反復条件 (t <= 0.1) が満たされている最後 (FINAL) の状態を出力せよという命令です*1。
2. シーケンス・シミュレーション
では、次にシーケンス・シミュレーションを組み込みましょう。 これは1つの物理系に対して、「ある時点までは何らかの反復条件で状態を更新し、それ以降は別の反復条件で状態を更新する」といった時に使います。 変更できるのは反復条件で、状態の更新方法(オイラー法など)ではありません。 データ出力は変更することができます。もう少し具体的な使い方として、何らかの平衡状態を調べたいときに、平衡状態に達するまでの反復条件(とデータ出力)と平衡状態に達してからの反復条件(とデータ出力)を変更するといったものがあります。 これはそのうち『計算物理学入門』に出てくるかと思います(まぁ、そこまで辿り着くことはできないと思いますが)。
今回は t=1 と t=2 での物理系の状態を出力させたい(それ以外の時間の状態を出力させない)ためにシーケンス・シミュレーションを使います。 以前に見た複合シミュレーション (composite simulation) を用いても行えますが、そこはシーケンス・シミュレーションの練習ってことで。
シーケンス・シミュレーションの書き方は、sequence ノード(もしくは type 属性に 'sequence' を設定した simulation ノード)の下に、今まで書いてきたような simulation ノードを複数書きます。 下記参照:
@GrabResolver('https://github.com/waman/groops-core/tree/master/repo') @Grab('org.waman.groops:groops-core:0.2-beta') import org.waman.groops.builder.SimulationBuilder import org.waman.groops.simulation.system.* new SimulationBuilder().sequence{ // new SimulationBuilder().simulation(type:'sequence'){ simulation{ system(new RadioactiveDecaySystem(), dt:0.1, lambda:1.0d) init(t:0.0, N:1.0d) continueWhile{ it.t <= 1.0 } console(outputTiming:OBSERVE_FINAL) } simulation{ continueWhile{ it.t <= 2.0 } console(outputTiming:OBSERVE_FINAL) } }.simulate() // 物理系の定義は省略
- problem2_7a1.groovy

- sequence ノード下の1つ目の simulation ノードは、今までの simulation ノードと同じです。
- sequence ノード下の2つ目の simulation ノードは、反復条件とデータ出力に関するノードのみを書きます。 system ノードがあっても(今のところは*2)無視します。 3つ目以降も同様に書けます。
この結果、t=1, t=2 での状態が出力されます。
3. さらに時間間隔を変えて並行シミュレーション
以上を踏まえて、さらに幾つかの時間間隔 dt の値に対して並行シミュレーションを行いましょう。 データもチャートに出力します。 問題ではシミュレーション結果と解析解との差を時間間隔 dt に対してプロットせよって話でしたね。 ちょっと込み入りますが、スクリプトはこんな感じ:@GrabResolver('https://github.com/waman/groops-core/tree/master/repo') @Grab('org.waman.groops:groops-core:0.2-beta') import org.waman.groops.builder.SimulationBuilder import org.waman.groops.simulation.system.* def N0 = 1.0d, lambda = 1.0d // 解析解 def analytic = { double t -> N0 * Math.exp(-lambda * t) } def N1 = analytic(1.0), N2 = analytic(2.0) println "N(1) = $N1, N(2) = $N2" // シミュレーションを行う時間間隔のリスト def dtList = [0.0125, 0.025, 0.05, 0.1, 0.2] new SimulationBuilder().parallel{ def pngout = png(fileName:'problem2_7a.png', overwrite:true){ chart(title:'Problem 2.7 a', domainLabel:'dt', rangeLabel:'N/N(0)'){ point(label:'t = 1', x:'dt', y:{ it.N - N1 }) point(label:'t = 2', x:'dt', y:{ it.N - N2 }) } } for(dt in dtList){ // この sequence ノードは上記のサンプルとほとんど同じ sequence{ simulation{ system(new RadioactiveDecaySystem(), dt:dt, lambda:lambda) init(t:0.0, N:N0) parameterObservableSet() continueWhile{ it.t <= 1.0 } console(dataEntries:['t', 'N'], outputTiming:OBSERVE_FINAL) output(pngout['t = 1'], outputTiming:OBSERVE_FINAL) } simulation{ continueWhile{ it.t <= 2.0 } console(dataEntries:['t', 'N'], outputTiming:OBSERVE_FINAL) output(pngout['t = 2'], outputTiming:OBSERVE_FINAL) } } } }.simulate() class RadioactiveDecaySystem extends AnnotationObservableSystem{ @State BigDecimal t @State double N @Parameter BigDecimal dt @Parameter double lambda @Override void evolve(Map<String, Object> params) { N -= lambda * N * dt.doubleValue() t += dt } }
シミュレーション結果は以下のようになります:
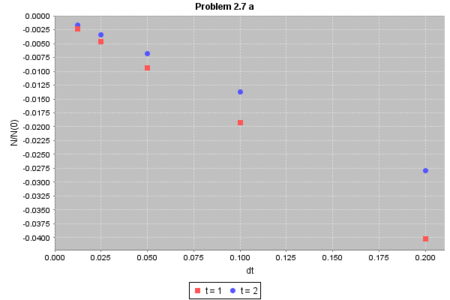
t=1, t=2 どちらでもシミュレーションの誤差が dt に比例することが分かりますね。 問題2.7の言葉では、この計算法は1次であるというのでした。 まぁ、同じオイラー法を使ってるので1次になるでしょうね。

- 作者: ハーベイゴールド,ジャントボチニク,Harvey Gould,Jan Tobochnik,鈴木増雄,石川正勝,溜渕継博,宮島佐介
- 出版社/メーカー: ピアソンエデュケーション
- 発売日: 2000/12
- メディア: 単行本
- 購入: 1人 クリック: 28回
- この商品を含むブログ (45件) を見る

- 作者: 関谷和愛,上原潤二,須江信洋,中野靖治
- 出版社/メーカー: 技術評論社
- 発売日: 2011/07/06
- メディア: 単行本(ソフトカバー)
- 購入: 6人 クリック: 392回
- この商品を含むブログ (155件) を見る