今回は問題 2.7 の続き。 放射性原子核を扱う場合、崩壊定数 よりも半減期
の方がよく使われるので、こちらを元にしたコードに書き換える問題です。
問題
a. プログラム cool を修正し、原子核崩壊で使われる表記に直せ。 そして、について、
と
のときの
の解析解の値とオイラー法の差を計算せよ。 さらに、それぞれの
の値では、その差が
に比例することを示せ。
b. 放射性崩壊の割合は、
ではなく半減期
程度の大きさを単位として与えると都合がよい。 半減期は最初の原子核の半数が崩壊する時間であり、
で与えられる。 修正したプログラムでこの関係を確かめよ。
の半減期が
年なら崩壊定数はいくらか。
c. 半減期を単位として時間を測るようにプログラムを書き換えよ。 そのプログラムで 100μg の [\tex:{ {}^{238}U }] が最初の量の20%に減少する時間を求めよ。
d. プログラムを2次のアルゴリズムに書き換えて、設問 a と c をもう一度行え。
b. 半減期をシミュレーションで求める
まずは前回に書いた、崩壊定数を用いたシミュレーション・スクリプトを変更して半減期@GrabResolver('https://github.com/waman/groops-core/tree/master/repo') @Grab('org.waman.groops:groops-core:0.2-beta') import org.waman.groops.builder.SimulationBuilder import org.waman.groops.simulation.system.* import java.awt.Color import static java.lang.Math.* def N0 = 1.0d, N_end = N0*0.5d def lambda = 1.0d new SimulationBuilder().simulation{ system(new RadioactiveDecaySystem(), dt:0.001, lambda:lambda) init(t:0.0, N:N0) continueWhile{ it.N > N_end } console(outputTiming:FINAL) png(fileName:'problem2_7b.png', overwrite:true){ chart(title:'Problem 2.7 b', domainLabel:'t', rangeLabel:'N/N(0)'){ dot(label:'Simulation', x:'t', y:'N') marker(label:'N / N0 = 1/2', y:0.5d, paint:Color.BLUE) marker(label:'T_1/2', x:log(2.0d)/lambda, paint:Color.GREEN) } } }.simulate() class RadioactiveDecaySystem extends AnnotationObservableSystem{ @State BigDecimal t @State double N @Parameter BigDecimal dt @Parameter double lambda @Override void evolve(Map<String, Object> params) { N -= lambda * N * dt.doubleValue() t += dt } }
- problem2_7b.groovy

- 物理系 RadioactiveDecaySystem は前回と同じです。
- 時間間隔 dt は 0.001 としています。
この結果、核数 N が半分になるまでにかかった時間は 0.693 でした。 dt が 0.001 なので精度は小数第3位まで。 途中の核数も合わせてチャートに出力すると以下のようになります:
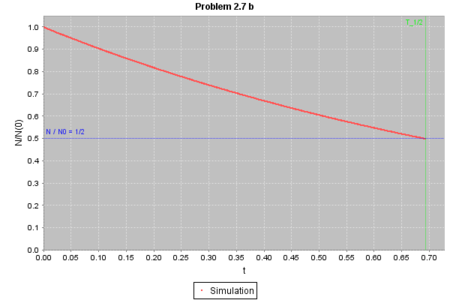
青の横線が核数 0.5 の線で、N の値がこの線の下に落ちるまで反復が繰り返されます。 緑の縦線は (*) 式から計算した半減期の値です:
赤い線(シミュレーション・データ)が青い線(N = 0.5)と交わる点で、緑の線(半減期の理論値)とも交わっていることが分かります。 よって、半減期と崩壊定数の関係を表す (*) 式がシミュレーションで確かめられました。
 の崩壊定数
の崩壊定数
(*) 式を
よって、半減期が 年なら、崩壊定数
は
となり、 /年
/秒 となります。 こんな値をシミュレーションで使うわけにもいかないのでどうしようか?というのが次の設問です。

- 作者: ハーベイゴールド,ジャントボチニク,Harvey Gould,Jan Tobochnik,鈴木増雄,石川正勝,溜渕継博,宮島佐介
- 出版社/メーカー: ピアソンエデュケーション
- 発売日: 2000/12
- メディア: 単行本
- 購入: 1人 クリック: 28回
- この商品を含むブログ (45件) を見る

- 作者: 関谷和愛,上原潤二,須江信洋,中野靖治
- 出版社/メーカー: 技術評論社
- 発売日: 2011/07/06
- メディア: 単行本(ソフトカバー)
- 購入: 6人 クリック: 392回
- この商品を含むブログ (155件) を見る