倭算数理研究所

科学・数学・学習関連の記事を、「倭マン日記」とは別に書いていくのだ！

トップ > commons-math > commons-math 解読 (18) : ガンマ関数 Gamma

commons-math 解読 (18) : ガンマ関数 Gamma

commons-math 特殊関数

前回に引き続き、今回も org.apache.commons.math.special パッケージのクラスを見ていきます。　今回はガンマ関数を表す Gamma クラス です。

Gamma クラス

Gamma クラスには、以下のような static フィールド、static メソッドが定義されています：

package org.apache.commons.math.special;

public class Gamma{

    public static final double GAMMA;

    public static double logGamma(double x){ ... }

    public static double digamma(double x){ ... }
    public static double trigamma(double x){ ... }
 
    public static double regularizedGammaP(double a, double x){ ... }
    public static double regularizedGammaP(double a, double x, double epsilon, int maxIterations){ ... }
    public static double regularizedGammaQ(double a, double x){ ... }
    public static double regularizedGammaQ(double a, double x, double epsilon, int maxIterations){ ... }
}

Gamma クラスで計算できるガンマ関数には以下のものがあります（オイラー定数は関数ではありませんが含めてます）：

  • オイラー定数 { \displaystyle \gamma }
  • ガンマ関数 { \displaystyle \Gamma(x) }
  • ポリガンマ関数系 { \displaystyle \psi_n(x) }
    • ディガンマ関数 { \displaystyle \Psi(x) \,(= \psi_0(x)) }
    • トリガンマ関数 { \displaystyle \psi_1(x) }
  • 不完全ガンマ関数系
    • 第1種不完全ガンマ関数 { \displaystyle \gamma(a,\,x) }
    • 第2種不完全ガンマ関数 { \displaystyle \Gamma(a,\,x) }
    • 正則化されたガンマ関数 { \displaystyle P(a,\,x),\,Q(a,\,x) }

太字のものが Gamma クラスで計算できる関数です。

オイラーの定数 ： Euler's constant

まずは Gamma クラスに定義されている定数、オイラーの定数 GAMMA （wikipedia:オイラーの定数）。

　　{ \displaystyle \begin{align*} \gamma &= \lim_{n\rightarrow\infty}\left(\sum_{k=1}^n\frac{1}{k} - \ln(n)\right) \\ &= 0.57721 56649 01532 86060 65120 90082 40243 10421 \\ &\qquad 59335 93992 35988 05767 23488 48677 26777 66467 \\ &\qquad 09369 47063 29174 67495\dots \end{align*} }

double の精度では { \gamma = 0.5772156649015329 } です。　ガンマ関数との関係は、後に出てくるディガンマ関数 { \Psi(x) } を用いて

　　{ \displaystyle \gamma = -\Psi(1) }

となっています。

ガンマ関数

ガンマ関数は積分を用いて以下のように定義されます：

　　{ \displaystyle \Gamma(x) = \int_0^\infty t^{x-1}e^{-t}dt }

ガンマ関数は、任意の自然数 n に対して

　　{ \displaystyle \Gamma(n+1) = n! }

が成り立つように、階乗を一般化した関数です。　従って、引数の値が大きくなればガンマ関数の値は指数関数的に増大します*1。　このためか、Gamma クラスではガンマ関数の値を直接返すメソッドは定義されてなくて、代わりにその対数値を返す logGamma() メソッドが定義されています。

ガンマ関数は引数が 0 もしくは負の整数でなければ値を持ちますが、引数が負であれば正負どちらの値もとります（引数が正ならガンマ関数の値も常に正）。　従ってガンマ関数の対数 { \log \Gamma(x) } は、引数が負の数だと値が実数にならない場合があります。　注意が必要なのは、logGamma() メソッドではガンマ関数の値が正負どちらでも、引数が 0 以下だと NaN が返されるようになっていることです。　引数が負の数でも、ガンマ関数の値が正になる場合はありますが*2、その場合でも logGamma() メソッドは NaN を返します。　もし引数が負の場合のガンマ関数の値が必要なら、ガンマ関数が満たす恒等式

　　{ \displaystyle \Gamma(x)\Gamma(1-x) = \frac{\pi}{\sin \pi x} }

を用いて計算することができます。

ポリガンマ関数 ： Polygamma Function

次は、ディガンマ関数やトリガンマ関数が属する類のポリガンマ関数を見ていきましょう。　ポリガンマ関数は、以下のようにガンマ関数の対数の微分で定義されます：

　　{ \displaystyle \begin{align*} \psi_n(x) &= \frac{d^{n+1}}{dz^{n+1}}\log\Gamma(x) = \frac{d^n}{dx^n}\left(\frac{\Gamma'(x)}{\Gamma(x)}\right) \end{align*} }

定義から、ポリガンマ関数は以下の漸化式を満たします：

　　{ \displaystyle \psi_{n+1}(x) = \frac{d}{dx}\psi_n(x) }

上記の logGamma() はポリガンマ関数で n = -1 の場合と思うこともできます：

　　{ \displaystyle \log\Gamma(x) = \psi_{-1}(x) }

ディガンマ関数 ： Digamma Function
Gamma クラスの digamma() メソッドはディガンマ関数の値を返します。　ディガンマ関数はポリガンマ関数の n = 0 の場合です：

　　{ \displaystyle \Psi(x) = \psi_0(x) = \frac{d}{dx}\log\Gamma(x) = \frac{\Gamma'(x)}{\Gamma(x)} }

ディガンマ関数は logGamma() の導関数です。

トリガンマ関数 ： Trigamma Function
Gamma クラスの trigamma() メソッドはトリガンマ関数の値を返します。　トリガンマ関数はポリガンマ関数の n = 1 の場合です：

　　{ \displaystyle \psi_1(x) = \frac{d^2}{dx^2}\log\Gamma(x) }

トリガンマ関数はディガンマ関数の導関数です。

logGamma(), digamma(), trigamma() メソッドが表す関数をグラフにすると下図のようになります：


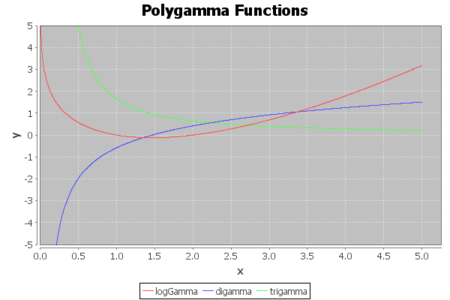
digamma(), trigamma() メソッドは logGamma() メソッドと同様に、引数が0以下だと NaN を返します。

不完全ガンマ関数 ： Incomplete Gamma Function

最後は不完全ガンマ関数の類を見ていきます：

  • 不完全ガンマ関数の定義
  • Γ関数との関係
  • 誤差関数との関係
  • 正則化されたガンマ関数

Gamma クラスに定義されているメソッドによって計算できるのは、最後の正則化されたガンマ関数 (regularized gamma function) です。

不完全ガンマ関数の定義
第1種不完全ガンマ関数 { \gamma(a,\,x) }、第2種不完全ガンマ関数 { \Gamma(a,\,x) } はそれぞれ以下のように定義されます：

　　{ \displaystyle \gamma(a,\,x) = \int_0^x t^{a-1}e^{-t}dt ,\qquad \Gamma(a,\,x) = \int_x^\infty t^{a-1}e^{-t}dt }

積分区間が不完全なんですね。　ガンマ関数の引数 { x } に対応するものは、不完全ガンマ関数では { a } になっていることに注意。　{ x } は積分区間に現れています。

ガンマ関数との関係
不完全ガンマ関数は、定義より以下の恒等式が成り立ちます：

　　{ \displaystyle \begin{align*} &\lim_{x\rightarrow\infty}\gamma(a,\,x) = \Gamma(a,\,0) = \Gamma(a) \\[2mm] & \gamma(a,\,x) + \Gamma(a,\,x) = \Gamma(a) \end{align*} }

第1種、第2種の不完全ガンマ関数は、ガンマ関数に関して相補的な関係にあります。

誤差関数との関係
不完全ガンマ関数は前回見た誤差関数 erf(x)、相補誤差関数 erfc(x) とも関係があります：

　　{ \displaystyle \begin{align*} \gamma(\tfrac{1}{2},\,x) = \sqrt{\pi} \, {\rm erf}\left(\sqrt{x}\,\right) ,\qquad \Gamma(\tfrac{1}{2},\,x) = \sqrt{\pi} \, {\rm erfc}\left(\sqrt{x}\,\right) \end{align*} }

これらの関係は、不完全ガンマ関数の定義に現れている積分変数を適当に変換すれば簡単に示せます。

正則化されたガンマ関数 ： Regularized Gamma Function
上で定義された不完全ガンマ関数を用いて、正則化されたガンマ関数 { P(a,\,x),\,Q(a,\,x) } は以下のように定義されます：

　　{ \displaystyle P(a,\,x) = \frac{\gamma(a,\,x)}{\Gamma(a)} ,\qquad Q(a,\,x) = \frac{\Gamma(a,\,x)}{\Gamma(a)} }

不完全ガンマ関数が満たす式より、2つの正則化されたガンマ関数は互いに相補的な関係にあることが分かります：

　　{ \displaystyle P(a,\,x) + Q(a,\,x) = 1 }

{ P(a,\,x),\,Q(a,\,x) } を、いくつかの { a } の値 (0.5, 1, 2) についてプロットすると下図のようになります：


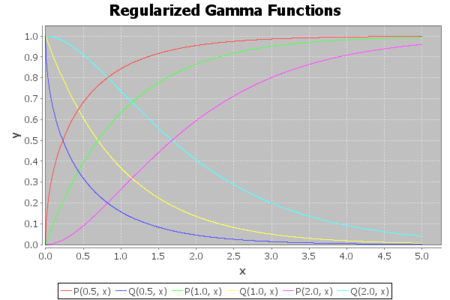
どちらの引数 { a,\,x } も正でないといけないようですね。

ふぅ、ガンマ関数、大変だ。　ベータ関数できるかなぁ。

*1:スターリングの公式など参照。

*2:m = 1, 2, 3, ・・・ として -2m < x < -2m+1 の区間