シュレディンガー方程式を解こう～井戸型ポテンシャルによる束縛状態～

シュレディンガー方程式を解こうシリーズ（目次）。　今回は1次元で井戸型ポテンシャルによって束縛状態になっている系を解いてきます。

　　 ${ \displaystyle\begin{align*} \left(-\frac{\hbar^2}{2m}\frac{d^2}{d x^2} + V(x)\right)\psi(x) = E\psi(x) \end{align*}}$

でした（1次元で変数が1つなので、偏微分ではなく常微分にしています）。

【この記事の内容】

井戸型ポテンシャル
シュレディンガー方程式を解く
無限に高い井戸型ポテンシャルの場合
有限の高さの井戸型ポテンシャルの場合

【参考】

『Quantum Mechanics (Dover Books on Physics) (English Edition)』

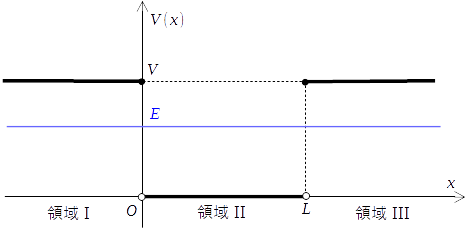
井戸型ポテンシャル

今回扱うポテンシャル ${ V(x) }$ は、幅 ${ L }$ 、高さ ${ V }$ の井戸型のポテンシャルです：

　　 ${ \displaystyle\begin{align*} V(x) = \begin{cases} 0 & (0 < x < L ) \\[2mm] V & (x \leqq 0,\,L \leqq x) \end{cases} \end{align*}}$

ポテンシャルは底を基準にして測っています。

シュレディンガー方程式を解く

今回は束縛状態のみを考えるので、系のエネルギー ${ E }$ はポテンシャルの高さ ${ V }$ より小さいとします：

　　 ${ \displaystyle\begin{align*} 0 < E < V \end{align*}}$

領域 I, II, III を上図のように分け、まずはそれぞれの部分でシュレディンガー方程式を解いていきます。

領域 I (x ≦ 0)

領域 I ではポテンシャルは定数 ${ V }$ です。　この領域での波動関数を ${ \psi_1(x) }$ とします。　まず、解として ${ \psi_1(x) = e^{\kappa_1 x} }$ の形の特解を求めましょう。　これをシュレディンガー方程式に代入して

　　 ${ \displaystyle\begin{align*} \left(-\frac{\hbar^2\kappa_1^2}{2m} + V\right) e^{\kappa_1 x} &= Ee^{\kappa_1 x} \\ \therefore \, \kappa_1 &= \pm\tfrac{\sqrt{2m(V-E)}}{\hbar} \end{align*}}$

を得ます。　以降、少々式を書くのが面倒なので ${ \kappa = \frac{\sqrt{2m(V-E)}}{\hbar} }$ とおきます。　一般解は特解の線形結合で表されるのでした：

　　 ${ \displaystyle\begin{align*} \psi_1(x) = A_1 e^{\kappa x} + B_1 e^{-\kappa x} \end{align*}}$

境界条件として ${ x \rightarrow -\infty }$ で波動関数が0となることを課すと、 ${ B_1 = 0 }$ となります。　よって、領域 I での波動関数は

　　 ${ \displaystyle\begin{align*} \psi_1(x) = A_1 e^{\kappa x} \qquad \left(\kappa = \tfrac{\sqrt{2m(V-E)}}{\hbar}\right) \end{align*}}$

となります。　定数 ${ A_1 }$ は、後ほど領域 II との接続条件から決めます。

領域 II (0 < x < L)

領域 II ではポテンシャルは0です。　この領域での波動関数を ${ \psi_2(x) }$ とします。　領域 I の場合と同様にして、解として ${ \psi_2(x) = e^{k_2 x} }$ の形の特解を求めましょう。　これをシュレディンガー方程式に代入して

　　 ${ \displaystyle\begin{align*} -\frac{\hbar^2 k_2^2}{2m} e^{\kappa_1 x} &= Ee^{k_2 x} \\ \therefore \, k_2 &= \pm i\tfrac{\sqrt{2mE}}{\hbar} \end{align*}}$

を得ます。　 ${ k = \frac{\sqrt{2mE}}{\hbar} }$ とおくと、領域 II での一般解は以下のようになります：

　　 ${ \displaystyle\begin{align*} \psi_2(x) = A_2 e^{ikx} + B_2 e^{-ikx} \end{align*}}$

領域 III (x ≧ L)

領域 III では領域 I と同じくポテンシャルは定数 ${ V }$ です。　この領域での波動関数を ${ \psi_3(x) }$ として、 ${ \psi_3(x) = e^{\kappa_3 x} }$ の形の特解を求めると

　　 ${ \displaystyle\begin{align*} \left(-\frac{\hbar^2\kappa_1^2}{2m} + V\right) e^{\kappa_3 x} &= Ee^{\kappa_3 x} \\ \therefore \, \kappa_3 &= \pm \kappa \qquad \left(\kappa = \tfrac{\sqrt{2m(V-E)}}{\hbar}\right) \end{align*}}$

となります。　 ${ \kappa }$ は領域 I で定義したものと同じです。　領域 III での一般解は

　　 ${ \displaystyle\begin{align*} \psi_3(x) = A_3 e^{\kappa x} + B_3 e^{-\kappa x} \end{align*}}$

となります。　境界条件として ${ x \rightarrow \infty }$ で波動関数が0となることを課すと、 ${ A_3 = 0 }$ となります。　よって、領域 III での波動関数は

　　 ${ \displaystyle\begin{align*} \psi_3(x) = B_3e^{-\kappa x} \qquad \left(\kappa = \frac{\sqrt{2m(V-E)}}{\hbar}\right) \end{align*}}$

となります。

接続条件を課す前の結果まとめ

上記の結果をまとめると、3つの領域での波動関数は以下のようになります：

　　 ${ \displaystyle\begin{align*} \psi(x) = \begin{cases} A_1 e^{\kappa x} & (x \leqq 0) \\ A_2 e^{ik x} + B_2 e^{-ikx} & (0 < x < L) \\ B_3 e^{-\kappa x} & (x \geqq L) \end{cases} \end{align*}}$

無限に高い井戸型ポテンシャルの場合

井戸の高さが有限の場合、接続条件を課すのが意外と大変なので、まずは簡単で有用な無限に高い井戸型ポテンシャルの場合をやっておきます。

領域 I, III での波動関数

${ V \rightarrow \infty }$ の場合 ${ \kappa \rightarrow \infty }$ となるので、波動関数が発散しないためには ${ A_1 = B_3 = 0 }$ でなければなりません。　つまり

　　 ${ \displaystyle\begin{align*} \psi_1(x) = \psi_3(x) = 0 \end{align*}}$

となります。

領域 II での波動関数とエネルギーの量子化

領域間で波動関数が連続であることを接続条件（境界条件）として課すと、領域 II の波動関数 ${ \psi(x) = A_2 e^{ik x} + B_2 e^{-ikx} }$ より

　　 ${ \displaystyle\begin{align*} \begin{cases} A_2 + B_2 = 0 \\ A_2 e^{ikL} + B_2 e^{-ikL} = 0 \end{cases} \end{align*}}$

これが自明でない解（ ${ A_2 = B_2 = 0 }$ でない解）を持つためには*1

　　 ${ \displaystyle\begin{align*} e^{ikL} - e^{-ikL} &= 0 \\ e^{2ikL} &= 1 \\ \therefore \, k &= \frac{n\pi}{L}\qquad\left(n = 1,\,2,\,3,\,\cdots\right) \end{align*}}$

となっていなければなりません。　 ${ k = \frac{\sqrt{2mE}}{\hbar} }$ だったので、このときのエネルギーは

　　 ${ \displaystyle\begin{align*} E &= \frac{\hbar^2}{2m}\left(\frac{n\pi}{L}\right)^2 \\ &= \frac{\hbar\pi^2}{2mL^2}n^2 \qquad(n = 1,\,2,\,3,\,\cdots) \end{align*}}$

のように飛び飛びの値しかとれなくなります。　つまり、エネルギーが量子化されます。

領域 II の波動関数

上記の ${ k }$ に対する条件が満たされているとき、領域 II の波動関数に対する2つの接続条件は同じ条件となり、 ${ A_2 + B_2 = 0 }$ となります。　よって領域 II での波動関数は

　　 ${ \displaystyle\begin{align*} \psi_2(x) &= A_2 e^{ikx} - A_2e^{-ikx} \\ &= 2iA_2 \sin kx \\ &= 2iA_2 \sin \frac{n\pi}{L}x \end{align*}}$

${ A_2 }$ は波動関数の規格化条件 ${ \int \left|\psi(x)\right|^2dx = 1 }$ から決められて

　　 ${ \displaystyle\begin{align*} \psi_2(x) = \sqrt{\frac{2}{L}}\;\sin\frac{n\pi}{L}x \end{align*}}$

を得ます。

まとめ

無限に高い井戸型ポテンシャルの場合の波動関数とエネルギー準位をまとめておくと

　　 ${ \displaystyle\begin{align*} \psi(x) &= \begin{cases} \sqrt{\dfrac{2}{L}}\;\sin\dfrac{n\pi}{L}x & (0 < x < L) \\[2mm] 0 & (x \leqq 0,\,L \leqq x) \end{cases} \\[2mm] E_n &= \frac{\hbar\pi^2}{2mL^2}n^2 \qquad(n = 1,\,2,\,3,\,\cdots) \end{align*}}$

となります。

有限の高さの井戸型ポテンシャルの場合

無限に高い井戸型ポテンシャルの場合と同様にして、有限の高さの井戸型ポテンシャルの場合にも接続条件を課して波動関数を求めてみましょう。　この場合もエネルギーが量子化されますが、エネルギーの具体的な表式を初等関数で表すことはできません。

接続条件とエネルギーの量子化

領域 I, II, III の境界 ${ x = 0,\,L }$ で波動関数とその座標微分が連続であることを接続条件（境界条件）として課しましょう。

${ x = 0 }$ での接続条件より

　　 ${ \displaystyle\begin{align*} A_1 &= A_2 + B_2 \qquad\cdots(1) \\ \kappa A_1 &= ik(A_2 - B_2) \qquad\cdots(2) \end{align*}}$

${ x = L }$ での接続条件より

　　 ${ \displaystyle\begin{align*} A_2e^{ikL} + B_2e^{-ikL} &= B_3e^{-\kappa L} \qquad\cdots(3) \\ ik(A_2e^{ikL} - B_2e^{-ikL}) &= -\kappa B_3e^{-\kappa L} \qquad\cdots(4) \end{align*}}$

${ A_1,\,A_2,\,B_2,\,B_3 }$ を変数として、これら4つの式を解いてみましょう。　(1), (2) 式より ${ A_1 }$ を消去して

　　 ${ \displaystyle\begin{align*} &\kappa(A_2 + B_2) = ik(A_2 - B_2) \\ \therefore \, &(\kappa-ik)A_2 + (\kappa+ik)B_2 = 0 \qquad\cdots (5) \end{align*}}$

また (3), (4) 式より ${ B_3 }$ を消去して

　　 ${ \displaystyle\begin{align*} &ik(A_2e^{ikL} - B_2e^{-ikL}) = -\kappa( A_2e^{ikL} + B_2e^{-ikL}) \\ \therefore \,& (\kappa + ik)A_2e^{ikL} + (\kappa - ik)B_2e^{-ikL} = 0 \qquad\cdots (6) \end{align*}}$

(5), (6) 式が自明でない解を持つためには、

　　 ${ \displaystyle\begin{align*} (\kappa + ik)^2 e^{ikL} &- (\kappa - ik)^2e^{-ikL} = 0 \\ (\kappa + ik) e^{ikL} & = \pm (\kappa - ik) \\ \kappa &= -ik\frac{e^{ikL}+1}{e^{ikL}-1},\,-ik\frac{e^{ikL}-1}{e^{ikL}+1} \\ &= -k\cot \frac{kL}{2},\,k\tan\frac{kL}{2} \end{align*}}$

ここで ${ -\cot(\theta+\frac{\pi}{2}) = \tan\theta }$ なので、 ${ \varphi = 0,\,\frac{\pi}{2} }$ として、上記の条件はまとめて書くことができます：

　　 ${ \displaystyle\begin{align*} &\kappa = -k\cot\left(\frac{kL}{2}+\varphi\right) \\ \therefore \, &\tan\left(\frac{kL}{2}+\varphi\right) = -\frac{k}{\kappa} \end{align*}}$

ここで ${ k = \frac{\sqrt{2mE}}{\hbar},\,\kappa = \frac{\sqrt{2m(V-E)}}{\hbar} }$ だったので、これは ${ E }$ の方程式となり、その解のみがエネルギーとしてとりうる値となります。　つまりエネルギーが量子化されます。　この方程式は解析的に解けないので、とりうるエネルギーの値を具体的に求められませんが、グラフを用いたり数値計算をしたりすれば数値的に求めることはできます。

V → ∞ の極限

定義より ${ \frac{k}{\kappa} = \sqrt{\frac{E}{V-E}} }$ なので、 ${ V \rightarrow \infty }$ の極限で上記の量子化条件は

　　 ${ \displaystyle\begin{align*} \tan\left(\frac{kL}{2}+\varphi\right) = 0 \end{align*}}$

となります。　これは簡単に解けて

　　 ${ \displaystyle\begin{align*} k = \frac{n\pi}{L} \qquad (n = 1,\,2,\,3,\cdots) \end{align*}}$

となり、無限に高い井戸型ポテンシャルの場合と同じ量子化条件が得られます。

波動関数

エネルギーが量子化されることが分かったので、別にもういい気もしますが、一応波動関数も求めておきましょう。

量子化条件が満たされているとき接続条件の (5), (6) 式は同じ条件式となるので、4つの変数 ${ A_1,\,A_2,\,B_2,\,B_3 }$ で条件式が3つとなって、変数1つだけを残して他が決まります。　ここでは ${ A_1,\,B_2,\,B_3 }$ を ${ A_2 }$ で表すことにし、 ${ A_2 }$ を含む定数を改めて ${ \mathcal{N} }$ と定義し直すと以下のようになります：

　　 ${ \displaystyle\begin{align*} psi(x) = \begin{cases} \mathcal{N}ke^{\kappa x} & (x \leqq 0) \\[2mm] \mathcal{N}(\kappa\sin kx + k\cos kx) & (0 < x < L) \\[2mm] \mathcal{N}(\kappa\sin kL + k\cos kL)e^{-\kappa (x-L)} & (x \geqq L) \end{cases} \end{align*}}$

後は規格化条件から ${ \mathcal{N} }$ を決めれば波動関数が求まりますが、結構複雑な式になるのでここで止めます。

補足

ここでは接続条件を「波動関数とその微分が境界で連続」としましたが、各境界で2つずつ条件式が出てくるのと、接続条件からは規格化定数（上記の ${ \mathcal{N} }$ ）が決まらないことは分かっていることから、この接続条件の代わりに「対数微分の値が境界で等しい」という条件を課す方が簡単になります。　波動関数の対数微分は

　　 ${ \displaystyle\begin{align*} \frac{d}{dx} \ln \psi(x) = \frac{\frac{d\psi(x)}{dx}}{\psi(x)} \end{align*}}$

となって、今の接続条件が満たされれば波動関数とその微分が等しく（まぁ比が等しいことしか言えませんが）、かつ規格化定数が分母分子で打ち消し合って接続条件に寄与しないことがわかります。

この接続条件は、今の井戸型ポテンシャルの場合には

　　 ${ \displaystyle\begin{align*} \begin{cases} \left.\dfrac{d}{dx} \ln \psi_1(x)\right|_{x = 0} = \left.\dfrac{d}{dx} \ln \psi_2(x)\right|_{x = 0} \\[2mm] \left.\dfrac{d}{dx} \ln \psi_2(x)\right|_{x = L} = \left.\dfrac{d}{dx} \ln \psi_3(x)\right|_{x = L} \end{cases} \end{align*}}$

となります。

では実際に接続条件を計算してみましょう。　まずは各領域の波動関数に対して対数微分を計算してみると

　　 ${ \displaystyle\begin{align*} \frac{d}{dx}\ln \psi_1(x) &= \kappa \\ \frac{d}{dx}\ln \psi_2(x) &= ik \frac{A_2 e^{ikx} - B_2 e^{-ikx}}{A_2 e^{ikx} + B_2 e^{-ikx}} \\ \frac{d}{dx}\ln \psi_3(x) &= -\kappa \end{align*}}$

となるので（領域 I, III では非常に簡単になりますね！）、接続条件は以下のようになります：

　　 ${ \displaystyle\begin{align*} \kappa &= ik \frac{A_2 - B_2}{A_2 + B_2} \\ -\kappa &= ik \frac{A_2e^{ikL} - B_2e^{-ikL}}{A_2e^{ikL} + B_2e^{-ikL}} \\ \end{align*}}$