単位球体内の一様分布を生成する方法を見ていくシリーズ(目次)。 今回は3次元。 やることは2次元の場合と同じ。 ちなみに3次元の単位球体は普通の「球」です。
極座標
3次元の極座標は以下のように与えられるのでした:
単位球内での積分は以下のようになります:
一様分布する変数
一様分布する変数への変数変換は以下の通り:
このとき、単位球体内の積分は以下のようになります:
直交座標の計算
極座標の変数を一様分布する変数で表すと
となるので、直交座標は以下のようになります:
これを用いて3次元球体内の一様乱数を生成するには、効率化のために に3を吸収させて(定義域にも)、以下のようにします:
ただし、変数 に対して
を区間
間に一様分布する変数とします。
Java コード
実際に Java で3次元球体内の一様乱数を生成してみましょう。 Java コードは以下のようになります:import static java.lang.Math.*; public class UniformDistributionB3{ public static void main(String... args){ for(int i = 0; i < 30000; i++){ double r = cbrt(random()); double cosTheta = random() * 2 - 1; double sinTheta = sqrt(1- cosTheta*cosTheta); double phi = random() * 2 * PI; double x = r * sinTheta * cos(phi); double y = r * sinTheta * sin(phi); double z = r * cosTheta; System.out.println(x+" "+y+" "+z); } } }
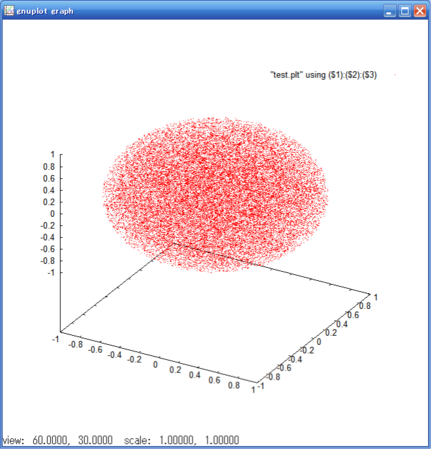
結果をプロットすると下図のようになります:
![[改訂新版]C言語による標準アルゴリズム事典 (Software Technology) [改訂新版]C言語による標準アルゴリズム事典 (Software Technology)](https://m.media-amazon.com/images/I/51O9Tl-XHyL._SL500_.jpg)