倭算数理研究所

科学・数学・学習関連の記事を、「倭マン日記」とは別に書いていくのだ！

トップ > 量子コンピューティング > Go で量子鍵配送 (Quantum Key Distribution) もう少し BB84 プロトコル

Go で量子鍵配送 (Quantum Key Distribution) もう少し BB84 プロトコル

量子コンピューティング Go

Go で量子コンピューティングシリーズ（目次）。　今回は前回見た BB84 プロトコルの特徴をもう少し詳しく見ていきます。

【この記事の内容】

長さ n の鍵を生成するために必要な qubit 数

アリスとボブは qubit 列の送受信を行った後に測定に使用した基底の情報を交換し、同じ基底で測定したビットのみを鍵のビットとして使用するので、n ビットの鍵を生成するには n 個以上の qubit が必要となります。

理論的には、アリスとボブがそれぞれ五分五分の確率で標準基底もしくはアダマール基底で測定するので、両者の基底が一致するのは50%です。　よって n ビットの鍵を生成するには平均 2n 個の qubit が必要となります。

これを前回までのコードを元にシミュレーションしてみると、（Alice や qkd.AppendMatchingBits 関数を変更する必要があるのでコードは載せませんが、一応 GitHub のリポジトリ内のどこかにあります）確かに約50%となります。
github.com

盗聴に気づく確率

量子鍵配送では量子チャネルに送られた qubit を測定されただけで、アリスとボブは盗聴されていることに気づくことができる場合があります。　鍵の長さが長いほど盗聴に気づく可能性は高くなり、理論的には鍵の長さが { n } のとき盗聴に気づく確率 { P_n } は

　　{ \displaystyle\begin{align*} P_n = 1 - \left(\frac{3}{4}\right)^n \end{align*}}

で与えられます（「『Quantum Computing: A Gentle Introduction』の演習問題を解く 2.9」参照）。　この確率が90%を始めて越えるのは { n = 9 } のときです（ { n = 8 } のとき { P_8 = 0.8998... } ですが）。

では、これをシミュレーションしてみましょう。　量子チャネルに送られた qubit を測定するだけのイヴは前回の記事にコードを載せましたが、他の量子鍵配送プロトコルでも使えるので qkd パッケージに定義することにします：

package qkd

// NewObservingEve 関数は、送られた qubit を測定だけするイヴを返します。
func NewObservingEve() Eve {
  return &observingEve{make(chan struct{})}
}

type observingEve struct {
  done chan struct{} 
}

func (eve *observingEve) Stop(){ eve.done <- struct{}{} }

func (eve *observingEve) Eavesdrop(ch *InternalOfChannel) {
  loop:
    for {
      select {
        case qbts := <-ch.QubitsFromAlice():
          // 量子チャネルで送られた qubit 列を標準基底もしくはアダマール基底で
          // ランダムに測定する
          bases := NewRandomBits(len(qbts))
          for i, qbt := range qbts {
            if bases[i] {
             qbt.ObserveInHadamardBasis()
            } else {
              qbt.ObserveInStandardBasis()
            }
          }
          ch.QubitsToBob() <- qbts

        case bits := <-ch.FromBob():
          ch.ToAlice() <- bits

        case bits := <-ch.FromAlice():
          ch.ToBob() <- bits

        case <-eve.done:
          break loop
        }
      }
}

このイヴを使って、鍵の長さ (nKey) を5～15まで変えてアリスとボブが盗聴に気づく確率をシミュレーションすると（各鍵の長さで10000回試行）

  rand.Seed(time.Now().UnixNano())

  const nTry = 10000
  for nKey := 5; nKey <= 15; nKey++ {
    matched := 0  // アリスとボブの鍵が一致した回数（盗聴に気づかなかった回数）
    for i := 0; i < nTry; i++ {
      // イヴに盗聴されているもとでの鍵の確立
      aliceKey, bobKey, _ := qkd.EstablishKeysWithEavesdropping(
        NewAlice(nKey), NewBob(nKey), qkd.NewObservingEve())

      if aliceKey.Equals(bobKey) { matched++ }
    }
    fmt.Printf("%d: %.3f\n", nKey, 1-float32(matched)/float32(nTry))
    // 盗聴に気づく確率は 1 - (matched/nTry)
  }

（qkd.EstablishKeysWithEavesdropping 関数については『Go で量子鍵配送 (Quantum Key Distribution)』参照。　内容を追記しています）結果は

5: 0.767
6: 0.835
7: 0.865
8: 0.907
9: 0.916
10: 0.948
11: 0.948
12: 0.960
13: 0.976
14: 0.981
15: 0.988

となって、n = 8 あたりで90%になって理論値と概ね一致します。　gonum plot を使ってグラフにしておくと（少し鍵の長さを増やしてます）

f:id:waman:20171104022132p:plain

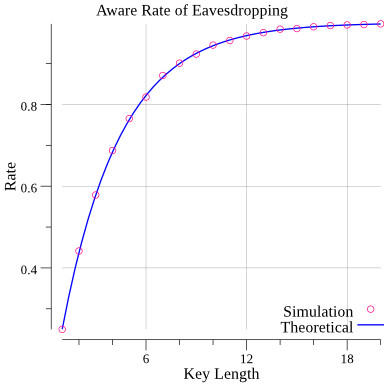
のようによく一致しているのが分かります（誤差評価はしてませんが）。

イヴが正しい鍵のビット値を得る割合

次はイヴが盗聴した情報を基に鍵を生成したとき、どの程度鍵の正しいビット値を得ることができるかを見ていきます。

イヴは盗聴した qubit を標準基底もしくはアダマール基底で測定し、測定結果が { |0\rangle,\,|+\rangle } なら0、 { |1\rangle,\,|-\rangle } なら1とデコードして（ボブと同じ）、鍵のビット値を生成します。　このビット値が確実に正しいかどうかは、その後の古典チャネルを盗聴してアリスとボブの使用した基底と等しいかどうかで判定できます。

鍵を生成するイヴの実装は以下のようになります：

// NewEve は盗聴した鍵を取得できるイヴを生成します。
func NewEve(n int) *Eve {
  return &Eve{n, nil, nil, make(chan struct{})}
}

type Eve struct {
  n int
  key qkd.Key
  sureKeyBits []bool  // 確実に正しい鍵のビット（true の位置の key のビット値は確実に正しい）
  done chan struct{}
}

func (eve *Eve) Key() qkd.Key {	return eve.key }
func (eve *Eve) Stop(){ eve.done <- struct{}{} }

// SureKeyBitCount メソッドは、イヴが確実に正しいと分かる鍵のビット値の個数を返します。
func (eve *Eve) SureKeyBitCount() int {
  sure := 0
  for i := 0; i < eve.n; i++ {
    if eve.sureKeyBits[i] { sure++ }
  }
  return sure
}

func (eve *Eve) Eavesdrop(ch *qkd.InternalOfChannel) {
  var keyBits   []bool  // イヴがデコードした鍵ビット
  var bases     []bool  // イヴが測定に使用した基底
  var matchesBE []bool  // イブとボブの基底が一致していたかどうか
  loop:
    for {
      select {
      case qbts := <-ch.QubitsFromAlice():
        keyBits = make([]bool, len(qbts))
        bases = qkd.NewRandomBits(len(qbts))
	
        for i, qbt := range qbts {
          if bases[i] {
            keyBits[i] = qbt.ObserveInHadamardBasis() == ket.Minus()
          } else {
            keyBits[i] = qbt.ObserveInStandardBasis() == ket.One()
          }
        }
        ch.QubitsToBob() <- qbts
	
      case bobBases := <-ch.FromBob():
        matchesBE = matchBases(bases, bobBases)  // イヴとボブの基底が一致していたかどうか
        ch.ToAlice() <- bobBases
	
      case matches := <-ch.FromAlice():
        eve.key = qkd.AppendMatchingBits(eve.key, keyBits, matches, eve.n)
        eve.sureKeyBits = qkd.AppendMatchingBits(eve.sureKeyBits, matchesBE, matches, eve.n)
        ch.ToBob() <- matches
	
      case <-eve.done:
        break loop
      }
    }
}
  • matchBases 関数、qkd.AppendMatchingBits 関数は前回の記事参照。　意外と使い回しができたw
  • イヴが確実に正しいビットの位置を得る方法を簡単に見ておきましょう。　イヴは、まず自分が使用した基底とボブから送られてくるボブの使用した基底と比べて、一致していたかどうかを matchesBE に保持します。　次にアダムから送られてくるアリスとボブの基底が一致していたかどうかの情報から、最終的な鍵のビット値でイヴが確実に正しいと分かるものを特定し、イヴのフィールド sureKeyBits に追加します。

このイヴの実装を用いて、イヴが確実に正しい鍵のビット値を得る割合と、正しいビット値を得る平均的な割合をシミュレーションで計算してみましょう。　理論値は「『Quantum Computing: A Gentle Introduction』の演習問題を解く 2.9」を参照。

盗聴に気づいているときも含む場合
まずはアリスとボブの生成した鍵が異なっていて盗聴に気づくときも含めた場合。　確実に正しいと分かる鍵ビットの数は上記のイヴの SureKeyBitCount メソッドから分かり、一方、イヴの鍵ビットが平均的にどのくらい正しいかは、Key 型の ConcordanceRate メソッド（『Go で量子鍵配送 (Quantum Key Distribution)』参照。追記しました。単に2つの bool スライスでビット値が等しい割合を計算するだけ）を使えば分かります。　長さ100000の鍵を生成してそれぞれを計算するコードは以下のようになります：

  rand.Seed(time.Now().UnixNano())

  nKey := 100000
  eve := NewEve(nKey)
  aliceKey, bobKey, eveKey := qkd.EstablishKeysWithEavesdropping(
    NewAlice(nKey), NewBob(nKey), eve)

  fmt.Printf("イヴが確実に正しいと分かる鍵ビット数: %.3f\n",
        float32(eve.SureKeyBitCount())/float32(eve.n))

  fmt.Printf("アリスとボブの鍵の一致率: %.3f\n", aliceKey.ConcordanceRate(bobKey))
  fmt.Printf("アリスとイヴの鍵の一致率: %.3f\n", aliceKey.ConcordanceRate(eveKey))
  fmt.Printf("ボブとイヴの鍵の一致率: %.3f\n", bobKey.ConcordanceRate(eveKey))

盗聴に気づく場合も含めているので、アリスとボブの鍵も異なるビットを含みます。　したがってこれらの一致率も表示するようにしています。　これを実行すると

イヴが確実に正しいと分かる鍵ビット数: 0.499  // 理論値は 50%
アリスとボブの鍵の一致率: 0.750
アリスとイヴの鍵の一致率: 0.748
ボブとイヴの鍵の一致率: 0.750  // 理論値は 75%

となり、理論値をうまく再現していますね。　ちなみに、アリス、ボブ、イヴの3者のうち、任意の2人の鍵の一致率が全て75%になるようです。

盗聴に気づいていない場合
次は、アリスとボブの鍵が一致して、イヴが盗聴していることに気づかない場合に、イヴが確実に正しいと分かる鍵ビットの数とイヴの鍵ビットが正しい平均的な割合をシミュレーションで計算してみましょう。　今の場合は各試行で盗聴に気づくかどうか（アリスとボブの鍵が一致していないかどうか）を判定しないといけないので、鍵の長さを10として100000回の試行を行うことにします（盗聴に気づかれない確率は10%以下なので、試行回数は実質10000回以下ですが）：

  nTry := 100000
  nKey := 10

  n := 0  // 盗聴に気づかれなかった回数
  sure := 0  // イヴが確実に正しいと分かるビット数
  conc := 0  // アリスとイヴの鍵ビットでビット値が一致していた数

  for i := 0; i < nTry; i++ {
    eve := NewEve(nKey)
    aliceKey, bobKey, eveKey := qkd.EstablishKeysWithEavesdropping(
      NewAlice(nKey), NewBob(nKey), eve)

    if aliceKey.Equals(bobKey) {
      n++
      sure += eve.SureKeyBitCount()
      conc += aliceKey.Concordance(eveKey)
    }
  }

  base := float32(n*nKey)
  fmt.Printf("イヴが確実に正しいと分かる鍵ビット数: %.3f\n", float32(sure)/base)
  fmt.Printf("アリスとボブの鍵の一致率: %.3f\n", float32(conc)/base)

これを実行すると

イヴが確実に正しいと分かる鍵ビット数: 0.66828305  // 理論値 66.7%
アリスとボブの鍵の一致率: 0.8350036  // 理論値 83.3%

となって理論値と大体合ってますね。　盗聴に気づかれる場合を落としているので、実質的な試行回数が少なくなって誤差が大きくなってますが。

さて、これで量子鍵配送 BB84 プロトコルの特徴がある程度数値的に分かりました。　次回以降の数回で、同様の解析をイヴの別の実装や別の量子鍵配送プロトコルでも計算して比較していきます。

Quantum Computing: A Gentle Introduction (Scientific and Engineering Computation)

Quantum Computing: A Gentle Introduction (Scientific and Engineering Computation)