Go で量子コンピューティングシリーズ(目次)。 今回は BB84 プロトコルで、アリスとボブがエンコード・デコードに使う基底をイヴが知らずに、ランダムな基底を使って盗聴を行う場合を見ていきます。 アリスとボブのコードは今までと同じです。
各種の理論値は「『Quantum Computing: A Gentle Introduction』の演習問題を解く 2.10」で計算しています。
イヴの実装
アリスとボブがエンコード・デコードに使う基底(標準基底・アダマール基底*1)をイヴが知らず、イヴはランダムな基底を用いて盗聴した qubit を測定するとしましょう。 ただし、ここでランダムな基底として使うのは、
で定められるものとします。 つまり、ブロッホ球面上の点で角度座標 が0のものだけを考えます*2。 この基底を使って盗聴した qubit を測定して、測定結果が
ならそれぞれ鍵ビットとして 0 (false),1 (true) を設定するとします。
以上のようなイヴの実装は次のようになります:
func NewEveR(n int) qkd.Eve { return &EveR{n, nil, make(chan struct{})} } type EveR struct { n int key qkd.Key done chan struct{} } func (eve *EveR) Key() qkd.Key { return eve.key } func (eve *EveR) Stop(){ eve.done <- struct{}{} } func (eve *EveR) Eavesdrop(ch *qkd.InternalOfChannel) { var keyBits []bool loop: for { select { case qbts := <-ch.QubitsFromAlice(): keyBits = make([]bool, len(qbts)) for i, qbt := range qbts { b := basis.NewRandomRealBasis() // ランダムな基底を生成 // 測定結果が |θ> なら 0 (false)、|θ⊥> なら 1 (true) を鍵ビットに設定 keyBits[i] = qbt.Observe(b) == b.Second() } ch.QubitsToBob() <- qbts case bobBases := <-ch.FromBob(): ch.ToAlice() <- bobBases case matches := <-ch.FromAlice(): // アリスとボブが鍵ビットとして採用したビットを eve.key に追加 eve.key = qkd.AppendMatchingBits(eve.key, keyBits, matches, eve.n) ch.ToBob() <- matches case <-eve.done: break loop } } }
- basis.NewRandomRealBasis 関数は上記で説明したランダムな基底を生成します(実装は割愛)。
- qkd.AppendMatchingBits 関数は前回までに出てきた関数と同じものです。
このイヴを使って盗聴した場合に、前回「Go で量子鍵配送 (Quantum Key Distribution) もう少し BB84 プロトコル」に計算した確率(割合)を同じように計算していきます。 ただし今の場合、アリスとボブが使った基底をイヴが知ることができず、イヴが確実に正しいビットを得たかどうかは分からないので、この量は計算しません。
アリスとボブが盗聴に気づく確率
アリスとボブがそれぞれ確立した鍵を比べて、異なっていれば qubit を盗聴されていることに気づきます。 理論的には、イヴがランダムな基底で測定を行っても、盗聴に気づかれる確率は前回と同じになります(「『Quantum Computing: A Gentle Introduction』の演習問題を解く 2.10」参照)。 つまり、n ビットの鍵を生成する場合、盗聴に気づく確率は
です。 盗聴に気づく確率が90%を越えるのは鍵の長さが9ビットのときです(8ビットでほとんど90%ですが)。
これを上記のイヴを使ってシミュレーションすると(イヴのインスタンス生成に NewEveR 関数を使っている以外は前回のコードと同じ)
rand.Seed(time.Now().UnixNano()) const nTry = 10000 for nKey := 5; nKey <= 15; nKey++ { matched := 0 for i := 0; i < nTry; i++ { aliceKey, bobKey, _ := qkd.EstablishKeysWithEavesdropping( NewAlice(nKey), NewBob(nKey), NewEveR(nKey)) if aliceKey.Equals(bobKey) { matched++ } } fmt.Printf("%d: %.3f\n", nKey, 1-float64(matched)/float64(nTry)) }
これを実行すると
5: 0.761 6: 0.817 7: 0.860 8: 0.899 9: 0.927 10: 0.946 11: 0.957 12: 0.966 13: 0.974 14: 0.984 15: 0.987
となり、前回と同じく n = 9 で始めて90%を越えています。 理論値とともにグラフにすると以下のようになります(少し n の範囲を増やしていますが):
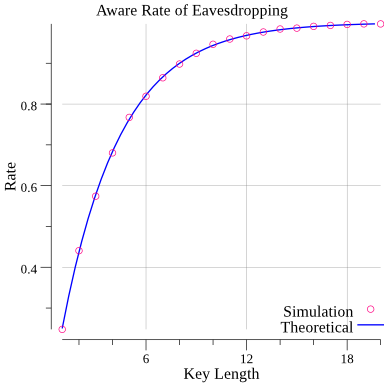
まぁ充分よく合っていますね。
イヴが正しいビット値を得る割合
次はイヴが盗聴して正しいビット値を得る割合(確率)をシミュレーションします。 前回と同じく、アリスとボブの鍵が一致せず盗聴に気づくときも含める場合と、鍵が一致して盗聴に気づかない場合を見ていきます。盗聴に気づいているときも含める場合
まずはアリスとボブが盗聴に気づいているときも含める場合。 アリスとイヴ、ボブとイヴの鍵が一致する割合の理論値は 65.9% です。 ちなみにアリスとボブの鍵の一致率は 75% です(上記の盗聴に気づく割合が前回と同じなのはこれが等しいため)。シミュレーションコードは以下のようになり
rand.Seed(time.Now().UnixNano()) nKey := 100000 aliceKey, bobKey, eveKey := qkd.EstablishKeysWithEavesdropping( NewAlice(nKey), NewBob(nKey), NewEveR(nKey)) fmt.Printf("アリスとボブの鍵の一致率: %.3f\n", aliceKey.ConcordanceRate(bobKey)) fmt.Printf("アリスとイヴの鍵の一致率: %.3f\n", aliceKey.ConcordanceRate(eveKey)) fmt.Printf("ボブとイヴの鍵の一致率: %.3f\n", bobKey.ConcordanceRate(eveKey))
これを実行すると
アリスとボブの鍵の一致率: 0.753 アリスとイヴの鍵の一致率: 0.661 ボブとイヴの鍵の一致率: 0.661
という結果が得られ、概ね理論値と一致します。
盗聴に気づかない場合
アリスとボブの鍵が一致して盗聴に気づいていない場合のイヴの鍵ビットの一致率もシミュレーションしておきましょう。 理論値は 71.2% です。前回と同じく鍵の長さを10ビットとしたシミュレーションコードは以下のようになり
rand.Seed(time.Now().UnixNano()) nTry := 100000 nKey := 10 n, conc := 0, 0 for i := 0; i < nTry; i++ { aliceKey, bobKey, eveKey := qkd.EstablishKeysWithEavesdropping( NewAlice(nKey), NewBob(nKey), NewEveR(nKey)) if aliceKey.Equals(bobKey) { n++ conc += aliceKey.Concordance(eveKey) } } fmt.Printf("アリスとイヴの鍵の一致率: %.3f\n", float32(conc)/ float32(n*nKey))
これを実行すると
アリスとイヴの鍵の一致率: 0.713
となって、これも理論値と概ね一致していますね。
以上の結果から、アリスとボブがエンコード・デコードに使っている基底をイヴが知らなければ、イヴが盗聴で得られる鍵ビットの一致率が低くなることが分かります。 ただし、盗聴に気づく確率は変わらないのも面白い性質ですね。

Quantum Computing: A Gentle Introduction (Scientific and Engineering Computation)
- 作者: Eleanor G. Rieffel,Wolfgang H. Polak
- 出版社/メーカー: The MIT Press
- 発売日: 2014/08/29
- メディア: ペーパーバック
- この商品を含むブログを見る