2次元のケプラー問題（斥力の場合）

古典力学のいろいろな系で運動方程式を解いていくシリーズ（目次）。　数回の記事で、万有引力を念頭に、逆2乗法則の引力の場合に2次元のケプラー問題の運動や軌跡を解きました。　今回は斥力の場合に運動や軌跡がどうなるかを見ていきます。　万有引力には斥力はありませんが、電磁気学では同様の力の法則（ポテンシャル）で斥力が存在するので普通に物理的な問題です。　ほとんどの計算は引力の場合と同じで ${ k }$ が ${ -k }$ に変わるだけなので、途中計算は間引きしてます。

中心力ポテンシャル

力が逆2乗法則に従う斥力となる中心力ポテンシャルは、 ${ k }$ を正の定数として

　　 ${ \displaystyle\begin{align*} V(r) = \frac{k}{r} \end{align*}}$

で与えられます。　引力の場合とは負符号が付いていないところが異なります。

軌跡の方程式

『中心力ポテンシャル中での質点の軌跡～2次元～』より、上記のポテンシャルのとき、軌跡の方程式は

　　 ${ \displaystyle\begin{align*} \theta - \theta_0 = - \frac{\ell}{\sqrt{2m}}\int \frac{du}{\sqrt{E - ku - \frac{\ell^2}{2m}u^2}} \qquad \left(u = \frac{1}{r}\right) \end{align*}}$

で与えられます。　右辺の積分は引力の場合と同様に実行できて

　　 ${ \displaystyle\begin{align*} \theta - \theta_0 &= - \sin^{-1}\left[\frac{1}{e}\left(\frac{a'(e^2 - 1)}{r} + 1\right)\right] \qquad \left(a' = \frac{k}{2E},\quad e = \sqrt{1+\frac{2E\ell^2}{k^2m}}\right) \end{align*}}$

これを ${ r }$ について解くと

　　 ${ \displaystyle\begin{align*} r = \frac{a'(e^2-1)}{e\sin(\theta_0 - \theta) - 1} \end{align*}}$

となります。　初期条件として ${ \theta_0 = 0 }$ で ${ r }$ が最小になることを課すと ${ \theta_0 = \frac{\pi}{2} }$ となるので、結局、軌道の方程式として以下を得ます：

　　 ${ \displaystyle\begin{align*} r = \frac{a'(e^2-1)}{e\cos\theta - 1} \end{align*}}$

${ r > 0 }$ より、偏角 ${ \theta }$ がとりうる範囲は

　　 ${ \displaystyle\begin{align*} -\alpha < \theta < \alpha \qquad\left(\alpha = \cos^{-1}\left(\frac{1}{e}\right)\right) \end{align*}}$

ただし、 ${ \cos^{-1}x }$ は値域が ${ 0 \leqq \cos^{-1}x \leqq \pi }$ となる分岐をとっています。

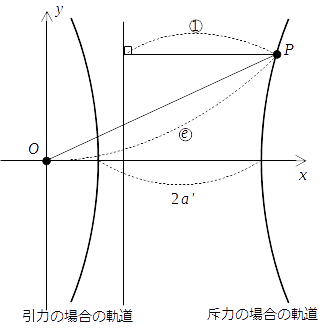
軌跡の図形

上記の軌跡の方程式は引力の場合と同じくやはり2次曲線の方程式で、斥力の場合は常に ${ E > 0 }$ なので離心率は ${ e > 1 }$ となり、双曲線であることが分かります。　引力で ${ E > 0 }$ の場合の双曲線は

　　 ${ \displaystyle\begin{align*} r = \frac{a'(e^2-1)}{e\cos\theta+1} \qquad \left(-\cos^{-1}\left(-\frac{1}{e}\right) < \theta < \cos^{-1}\left(-\frac{1}{e}\right) \right) \end{align*}}$

で与えられますが、これと斥力の場合の軌跡は（パラメータの値が同じ時に）双曲線の2つの連結部分それぞれに対応します*1。

動径方向の運動

軌跡が求まったので次は運動を求めてみましょう。　まずは動径方向の運動から。　『中心力ポテンシャル中での質点の運動方程式～2次元～』より、今の場合の中心力ポテンシャルでは、動径 ${ r }$ と時刻 ${ t }$ は

　　 ${ \displaystyle\begin{align*} t - t_0 &= \sqrt{\frac{m}{2}}\int \frac{dr}{ \sqrt{E - \frac{k}{r} - \frac{\ell^2}{2mr^2}}} \end{align*}}$

で関係づけられます。　右辺の積分を ${ R }$ とおくと

　　 ${ \displaystyle\begin{align*} R &= \int \frac{dr}{ \sqrt{E - \frac{k}{r} - \frac{\ell^2}{2mr^2}}} \\ &= \frac{1}{\sqrt{E}} \int \frac{rdr}{\sqrt{(r - a')^2 - a'^2e^2}} \end{align*}}$

となります。　ここで変数 ${ F }$ を

　　 ${ \displaystyle\begin{align*} r - a' = a'e\cosh F \qquad \left(r = a'(e\cosh F + 1),\qquad dF = a'e\sinh F dF\right) \end{align*}}$

で導入すると（ ${ F = 0 }$ のとき ${ r = a'(e + 1) }$ ）、上記の積分 ${ R }$ は

　　 ${ \displaystyle\begin{align*} R &= \frac{1}{\sqrt{E}} \int a'(e\cosh F + 1)dF \\ &= \sqrt{\frac{2a'^3}{k}} \left(e\sinh F + F\right) \qquad \left(\because a' = \frac{k}{2E}\right) \end{align*}}$

となり、結局、動径と時刻の関係は（初期条件 ${ t = 0 }$ で ${ r = a'(e+1)\quad(\Leftrightarrow F = 0) }$ も課して）

　　 ${ \displaystyle\begin{align*} t = \sqrt{\frac{ma'^3}{k}} \left(e\sinh F + F\right) \qquad \left(F = \cosh^{-1}\left(\frac{r-a'}{a'e}\right)\right) \end{align*}}$

を得ます。　引力で双曲線軌道をとる場合に導入した ${ \omega_+ = \sqrt{\frac{k}{ma'^3}} }$ を使うと

　　 ${ \displaystyle\begin{align*} \omega_+ t = e\sinh F + F \end{align*}}$

とも書けます。

動径について解く

上記の式の右辺 ${ e\sinh F + F }$ を ${ F }$ の関数とみたときの逆関数を ${ \tilde{F}_e(x) }$ と定義しましょう：

　　 ${ \displaystyle\begin{align*} \tilde{F}_e^{-1}(x) = e\sinh x + x \end{align*}}$

このとき、 ${ F }$ は ${ t }$ の関数として書けて

　　 ${ \displaystyle\begin{align*} F = \tilde{F}_e(\omega_+ t) \end{align*}}$

となります。　これを使うと動径が時刻の関数として解けて

　　 ${ \displaystyle\begin{align*} r(t) = a'\left(e\cosh \tilde{F}_e(\omega_+\; t) + 1\right) \end{align*}}$

を得ます。

ちなみに、引力の場合に導入した関数 ${ F_e(x) }$ は

　　 ${ \displaystyle\begin{align*} F_e^{-1}(x) = e\sinh x - x \end{align*}}$

で定義されていたことを踏まえて

　　 ${ \displaystyle\begin{align*} \tilde{F}_e^{-1}(x) &= e\sinh x + x \\ &= (-e)\sinh (-x) + (-x) \\ &= F_{-e}^{-1}(-x) \end{align*}}$

なので ${ \tilde{F}_e(x) = -F_{-e}(x) }$ という関係があります。

偏角方向の運動

動径方向の運動と軌跡の方程式を使うと偏角方向の運動は簡単に解けて

　　 ${ \displaystyle\begin{align*} \cos \theta &= \frac{a'(e^2-1) + r}{er} \\ &= \frac{e + \cosh \tilde{F}_e(\omega_+ t)}{e\cosh \tilde{F}_e(\omega_+ t) + 1} \end{align*}}$