2.6 コーヒーの冷却の問題：問題 2.1 コーヒーの冷却問題のためのプログラム（続き）

今回は『問題 2.1』の続きいきますよ?。

問題（再掲）

a. 電卓を使ってオイラー法でニュートンの冷却の法則の数値解を計算せよ。
b. 実験データに合う r の近似値を探せ。
c. 設問 b で見つけた r の値を使って、温度の時間変化をグラフに示せ。
d. シミュレーションで使った時間幅の値が結果に影響しないほど小さいことを確かめよ。
e. r の値はブラック・コーヒーとクリーム入りコーヒーでは同じか。
f. ニュートンの冷却の法則はコーヒーの冷却に適用できるか。
g. 温度差が 1/2, 1/4, 1/8 になるまでコーヒーが冷めるにはどれほどの時間がかかるか。

e.

クリーム入りコーヒーの冷却定数 r を求めます。　やり方はブラック・コーヒーの場合と同じです。　シミュレーション・コードは大体同じなので、CoolSystem の定義など、前回と変わりないものは省略します。　初期温度と実験データの使用している列が変わってますが、それ以外は同じです：

def rList = [0.020d, 0.022d, 0.024d, 0.026d, 0.028d, 0.030d]
def tmax = 46.0
def dt = 0.1

new SimulationBuilder().parallel{

    def pngout = png(fileName:'problem2_1e.png', overwrite:true){
        chart(title:'problem 2.1 e', domainLabel:'Time', rangeLabel:'Temperature', range:[30d, 75d]){
            for(r in rList){
                line(label:"r = $r", x:'time', y:'T')
            }
            marker(label:'Experiment', fileName:'data2_2.csv', x:0, y:2)
            // 実験データの使用列が変わってます
        }
    }

    for(r in rList){
        simulation(type:'composite'){
            simulation{
                system(new CoolSystem(), r:r, T_room:17d, dt:dt)
                init(time:0.0, T:68.8d)    // 初期温度が変わってます

                count(total:10)
            }
            continueWhile { it.time <= tmax }
            dataOutputter(pngout["r = $r"])
        }
    }

}.simulate()

シミュレーション結果は以下のようになります：

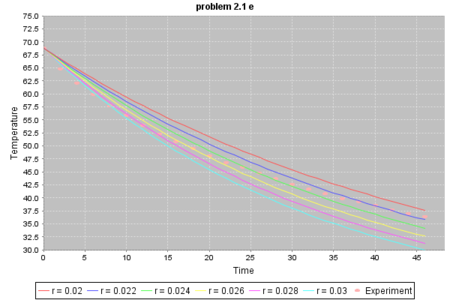
クリーム入りコーヒーの場合も全時間にわたって実験結果と一致する r の値はありませんでしたが、初期の時間帯ではブラック・コーヒーと同じく r = 0.03 のグラフがよく一致しているように見えます。　ってことで、ブラック・コーヒーでもクリーム入りコーヒーでも冷却定数 r の値は同じと思っていいでしょう。

ちなみに、こちらでもブラック・コーヒーのときと同じように、大まかに言って50?60℃くらいまではニュートンの冷却の法則が成り立っているように見えます。

f.

ブラック・コーヒーの場合もクリーム入りコーヒーの場合も、シミュレーションの初期では r = 0.03 とすれば実験データとよく合っています。　ただし時間が経って冷却が進むとどちらの場合も実験データとのズレが顕著になってきます。　ズレが大きくなってくる温度がどちらの場合も50?60℃のあたりであることは、偶然なのかたまたまなのか分かりませんがね:-P　ってことで、温度の範囲を制限すればニュートンの冷却の法則は成り立つってこといいんじゃねぇの？

ちなみに『wikipedia:ニュートンの冷却の法則』では、「温度差が極端に大きいときに成り立たない」となってるのに、温度差が小さいときに成り立たなくていいのかい？という根本的な疑問がありますが・・・　そもそも固体の冷却についての法則とか書いてるし(°д°)ェエ

g.

さて、最後は温度差が半分になるのにかかる時間の見積もり。　放射性原子核の半減期と同じですね。　放射性崩壊の話はこの章の最後に出てますが、やることは同じでしょう。　半減期の見積もり自体は難しくありませんが、これを機に composite シミュレーションと sequence シミュレーションという2つのシミュレーション・タイプを見ていきます。

Composite シミュレーションによる実装

まずは以前の記事でも出てきた Composite シミュレーション。　以前の記事では10回の反復を1単位にするのに使ってました。　今回は温度差が 1/2 や 1/4 になるまでの反復を1単位にするようにしてます。

@GrabResolver('https://github.com/waman/groops-core/tree/master/repo')
@Grab('org.waman.groops:groops-core:0.1-beta')

import org.waman.groops.builder.SimulationBuilder
import org.waman.groops.simulation.system.*

double T0 = 82.3d, T_room = 17.0d
def T_end = (T0 + T_room) / 2.0d

new SimulationBuilder().composite{    // .simulation(type:'composite'){ ... と同じ

    simulation(onIterationEnd:{ T_end = (T_end + T_room) / 2.0d }){
                    // onIterationEnd プロパティによって反復終了直後に処理を織り込む。
        system(new CoolSystem(), dt:0.1, r:0.03d, T_room:T_room)
        init(time:0.0, T:T0)
        
        continueWhile{ it.T >= T_end }
        console(dataEntries:['time', 'T'], outputTiming:FINAL)
    }
    count(total:5)    // 上の simulation ノードのシミュレーションを5回繰り返す。
}.simulate()

class CoolSystem extends AnnotationObservableSystem{

    @State BigDecimal time
    @State double T

    @Parameter BigDecimal dt
    @Parameter double T_room
    @Parameter double r
    
    @Override
    void evolve(Map params){
        T += -r * (T - T_room)*dt.doubleValue()
        time += dt
    }
}

problem2_1g.groovy
ちょっと込み入ったことをしている箇所は simulation ノードの onIterationEnd プロパティでしょうか。　これは内側の（simulation ノードの）シミュレーションの反復条件に使っている変数 T_end が、外側の（composite ノードの）シミュレーションの繰り返し5回で異なるためです。　ビルド・スクリプト中に（たとえば system ノードなどと同列に） T_end の値を変更する式を書くと、Simulator オブジェクトのビルド中にその演算が行われて、シミュレーションの実行中は最後の演算結果がずっと使われてしまうのでうまくいきません。　なので、実行中に T_end の値が変更されるように simulation ノードの onIterationEnd プロパティとして T_end の値を変えるクロージャを渡しています。　この処理が反復シミュレーションのどのタイミングで行われるのかはこちらの記事を参照。
console ノードに指定している outputTiming プロパティは結果を出力するタイミングを指定します。　このプロパティに指定できる値と出力されるタイミングについてはこちらを参照。

まぁ、ともかく結果は下表のようになります：

	時間	温度
1/2	23.1	49.62081079324095
1/4	46.2	33.29582384086412
1/8	69.3	25.14062766053315
1/16	92.3	21.078911691467592
1/32	115.4	19.037632565539088

温度差が半分になっていくのに同じだけの時間がかかっているのが分かります。

Sequence シミュレーションによる実装

次は、同様のシミュレーションを別アプローチで実装するもう一つの方法 Sequence シミュレーションを見ていきます。　よく考えるとあまり違いがないような気もしてきますが・・・　まぁ、Sequence シミュレーションは、もともとは平衡状態を扱うようなシミュレーションで、「平衡状態に達するまで」の反復と「平衡状態に達した後」の反復を別に書けるようにしよう！って目的のモノで、sequence ノード下の（simulation ノードなどで構築される）シミュレーションを順次実行していきます。　シミュレーション・コードは以下のようになります（Composite シミュレーションの場合と被っているコードは省略）：

double T0 = 82.3d, T_room = 17.0d
double T_end = (T0 + T_room) / 2.0d

new SimulationBuilder().sequence{    // .simulation(type:'sequence'){ ... と同じ

    simulation{
        system(new CoolSystem(), dt:0.1, T_room:T_room, r:0.03d)
        init(time:0.0, T:T0)

        continueWhile{ it.T >= T_end }
        console(outputTiming:FINAL)
    }

    4.times{
        simulation(onIterationStart:{ T_end = (T_end + T_room) / 2.0d }){
                        // onIterationStart プロパティによって反復開始直前に処理を織り込む！
            continueWhile{ it.T >= T_end }
            console(outputTiming:FINAL)
        }
    }

}.simulate()

Sequence シミュレーションでは、最初とそれ以降の simulation ノード（シミュレーションを構築するノード）の扱いが少々異なります。　1つ目の simulation ノードでは物理系や初期条件を構築するノード (system, init) を書くために、それ以降のノードと別扱いにしています。　2つ目以降の simulation ノードでは system, init ノードを書いていても無視されるので、実際にはまとめて書けなくもないんですが*1。
ここでも Composite シミュレーションの場合と同じく反復条件に使用する変数 T_end が各シミュレーションで異なるので、onIterationStart プロパティで処理を織り込んでいます。

実行結果は同じです。