2.8 簡単なグラフ表示：問題 2.4 冷却時間

今回はグラフ表示と緩和時間の計算です。　グラフ表示は今まで既に行っていますが、まぁ一応やっておきます。　緩和時間は放射性崩壊などの半減期と似た量です。

問題

a. プログラム cool を修正して、コーヒーの温度についての数値解を、数値として表示するのではなくグラフで示せ。
b. コーヒーの温度が、初期の温度と室温との差の ${ 1/e \sim 0.37 }$ に達するまでの時間を求めよ。　そのような時間を緩和時間という。　緩和時間は初期温度や室温に依存するか。　異なる ${ r }$ の値について計算を試み、緩和時間の ${ r }$ に対する定性的な依存性を求めよ。

a.

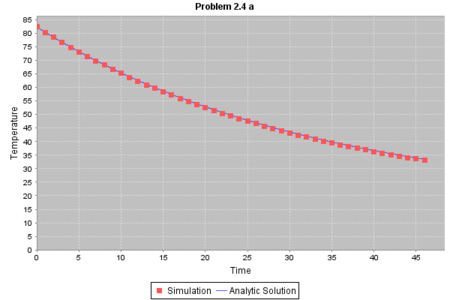
プログラム cool のグラフ表示は既にこちらで行っていますが、ここでももう一度やっておきましょう。　グラフを PNG ファイルとして生成するには png ノードとして書きます：

@GrabResolver('https://github.com/waman/groops-core/tree/master/repo')
@Grab('org.waman.groops:groops-core:0.1-beta')

import org.waman.groops.builder.SimulationBuilder
import org.waman.groops.simulation.system.*

double r = 0.03d, T_room = 17.0d, T0 = 82.3d

new SimulationBuilder().simulation{

    system(new CoolSystem(), r:r, T_room:T_room, dt:1.0)
    init(time:0.0, T:T0)
    continueWhile { it.time <= 46.0 }

    console()
    png(fileName:'problem2_4a.png', overwrite:true){
        chart(title:'Problem 2.4 a', domainLabel:'Time', rangeLabel:'Temperature'){
            point(label:"Simulation", x:'time', y:'T')
            marker(label:'Analytic Solution', function:{ t -> T_room - (T_room - T0)*Math.exp(-r*t) })
        }
    }
}.simulate()

class CoolSystem extends AnnotationObservableSystem{

    @State BigDecimal time
    @State double T

    @Parameter BigDecimal dt
    @Parameter double T_room
    @Parameter double r

    @Override
    void evolve(Map<String, Object> params) {
        T += -r * (T - T_room) * dt.doubleValue()
        time += dt
    }
}

problem2_4a.groovy

生成されるグラフは以下のようになります：

b.

次は緩和時間 (relaxation time) の計算。　まずは初期温度、室温、冷却定数を固定して行うシミュレーション・スクリプト：

@GrabResolver('https://github.com/waman/groops-core/tree/master/repo')
@Grab('org.waman.groops:groops-core:0.1-beta')

import org.waman.groops.builder.SimulationBuilder
import org.waman.groops.simulation.system.*

double r = 0.03d, T_room = 17.0d, T0 = 82.3d

double T_end = T_room + (T0 - T_room) / Math.E
println "r = $r, T_end = $T_end"

new SimulationBuilder().simulation{

    system(new CoolSystem(), r:r, T_room:T_room, dt:0.1)
    init(time:0.0, T:T0)
    continueWhile { it.T > T_end }

    console(dataEntries:['time', 'T'], outputTiming:OBSERVE_FINAL)
}.simulate()

class CoolSystem extends AnnotationObservableSystem{

    @State BigDecimal time
    @State double T

    @Parameter BigDecimal dt
    @Parameter double T_room
    @Parameter double r

    @Override
    void evolve(Map<String, Object> params) {
        T += -r * (T - T_room) * dt.doubleValue()
        time += dt
    }
}

problem2_4b1.groovy

緩和時間の精度は小数第1位までです（dt = 0.1 のため）。　このスクリプトでの実行結果より、緩和時間は 33.2 (min) でした。　ニュートンの冷却の法則を表す微分方程式の解析解は

　　 ${ \displaystyle \begin{align*} T(t) = T_s - (T_s - T_0) e^{-rt} \end{align*} }$

となるので（こちら参照）、緩和時間は冷却定数の逆数 ${ 1/r }$ になるはずです。　今のシミュレーションでは ${ r = 0.03 }$ としていたので、 ${ 1/r \sim 33.3 }$ となり、シミュレーション結果とだいたい一致しますね。

いろいろな室温 T_room, 初期温度 T0 で緩和時間を求めるシミュレーション・スクリプトは以下のようになります：

@GrabResolver('https://github.com/waman/groops-core/tree/master/repo')
@Grab('org.waman.groops:groops-core:0.1-beta')

import org.waman.groops.builder.SimulationBuilder
import org.waman.groops.simulation.*
import org.waman.groops.simulation.system.*

double r = 0.03d

new SimulationBuilder().parallel{
    for(T_room in (15..20)){
        for(T0 in (80..85)){
            simulation{
                system(new CoolSystem(), r:r, T_room:T_room, dt:0.1,
                       T_end:T_room + (T0 - T_room) / Math.E)
                init(time:0.0, T:T0)
                parameterObservableSet()
                console(format:"T_room : %s, T0 : $T0, Relaxation Time : %s", dataEntries:['T_room', 'time'],
                        outputTiming:FINAL, outputHeader:false)
            }
        }
    }
}.simulate()

class CoolSystem extends AnnotationControllableObservableSystem{

    @State BigDecimal time
    @State double T

    @Parameter BigDecimal dt
    @Parameter double T_room, r, T_end

    @Override
    void evolve(Map<String, Object> params) {
        T += -r * (T - T_room) * dt.doubleValue()
        time += dt
    }

    @Override
    boolean continueIteration(DataStore store){
        return T > T_end
    }
}

problem2_4b2.groovy
物理系を少し修正して、反復を停止する温度 T_end ( = T_room + (T0 - T_room) / e ) もシミュレーション・パラメータとして付け加えています。　また、反復の停止を物理系に判断させるために、物理系を AnnotationControllableObservableSystem のサブクラスとして作成しています。
標準出力にデータを出力をする console() ノードに format 属性を指定して、出力する文字列のフォーマットを設定しています。　「%s」には dataEntries 属性に指定された観測量の観測値が順に渡されます。

シミュレーション結果から、室温、初期温度を変えても緩和時間は変わらないことが分かります。　また、冷却定数を変えて同様のシミュレーションを行うと、冷却定数を ${ r }$ として緩和時間が ${ 1/r }$ であることも分かります。