倭算数理研究所

科学・数学・学習関連の記事を、「倭マン日記」とは別に書いていくのだ！

トップ > 電子回路 > RC 回路

RC 回路

電子回路

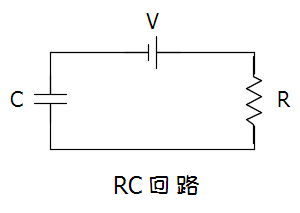
RC 回路は

  • 電源 （電源電圧 { V }）
  • 抵抗 （電気抵抗 { R }）
  • コンデンサ （電気容量 { C }）

からなります(下図参照)。


また、この回路の状態を規定する変数は

です。

微分方程式

コンデンサに蓄えられている電荷が { Q } のとき、

  • コンデンサにかかる電圧は { \frac{Q}{C} }
  • 回路に流れている電流は { \frac{dQ}{dt} } になるので、抵抗の電圧降下（かかる電圧）は { R\frac{dQ}{dt} }

よって各素子に加わる電圧の関係は

　　{ \displaystyle \begin{align*} V = \frac{Q}{C} + R\frac{dQ}{dt} \end{align*} }

となります。　これを少し変形すると

　　{ \displaystyle \begin{align*} R\frac{dQ}{dt} = V -\frac{Q}{C} \end{align*} }

が得られます。

解析解

RC 回路のしたがう微分方程式は「ニュートンの冷却の法則」の微分方程式と等価なので、解析解も同様に求めることができて、初期条件 { Q(0)=0 } のもとでは

　　{ \displaystyle \begin{align*} Q(t) = CV\left(1-e^{-\frac{t}{RC}}\right) \end{align*} }

となります。　ちなみに、初期条件 { Q(0) = Q_0 } のもとでは

　　{ \displaystyle \begin{align*} Q(t) = CV + (Q_0 - CV)\,e^{-\frac{t}{RC}} \end{align*} }

です。

計算物理学入門

計算物理学入門

  • 作者: ハーベイゴールド,ジャントボチニク,Harvey Gould,Jan Tobochnik,鈴木増雄,石川正勝,溜渕継博,宮島佐介
  • 出版社/メーカー: ピアソンエデュケーション
  • 発売日: 2000/12
  • メディア: 単行本
  • 購入: 1人 クリック: 28回
  • この商品を含むブログ (45件) を見る