数年前から高校数学で行列をやらなくなってグラフの回転ができなくなるなぁと思ってたんだけど*1、軌跡の問題だと思えば(言い張れば)今の高校数学の範囲内でグラフの回転を行うことができそうなので、実際にやってみます。 この記事内では回転は原点の周りの回転のみを扱います。
導出
回転したグラフの求め方は、基本的には前回導いたグラフの平行移動と同じですが、一般的に回転後のグラフの方程式は
のような形で与えられるとします。 例えば、中心が原点、半径が の円の方程式は
なので
です。
点を回転したときの座標の変換則を導く
まずは、任意の点を原点の周りに原点 以外の任意の点
をとり、線分
の長さを
、
と
の正の部分がなす角を
とします:
また、この点 を原点の周りに反時計回りに
だけ回転した後の点を
とします。
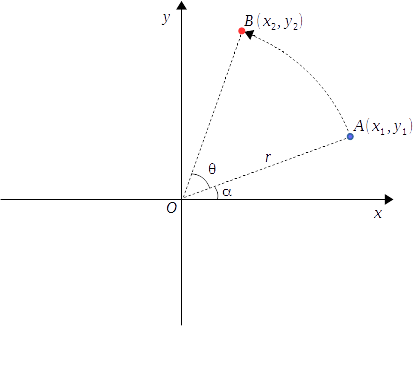
このとき、
結果をまとめると、変換則は以下のようになります:
変換前の座標を変換後の座標で表す
上記の変換則を逆に解いて
となります*2。
回転後のグラフの方程式を求める
以上を踏まえて、グラフを回転させてみましょう。 回転させたいグラフの方程式が
を満たします。これを(1)式に代入すると
よって のグラフを原点の周りに
だけ回転したグラフの方程式は
で与えられます。
使ってみよう
数学III の2次曲線で出てくる双曲線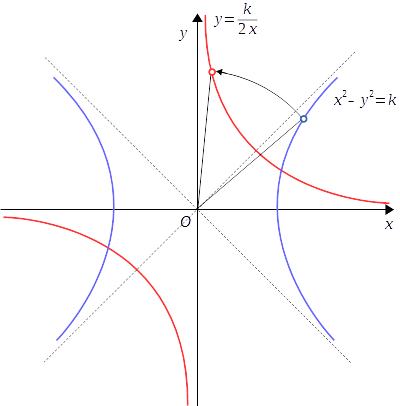
この場合、
となります。
よって回転後の双曲線の方程式は
となって、 が
に反比例する式が導けました。