懸垂曲線の方程式を導く - 倭算数理研究所

ひもの両端を持って垂らしたときにできる曲線を懸垂曲線（wikipedia:カテナリー曲線 catenary）といいますが、この曲線の方程式を導いてみます。　結果は双曲線関数の1つ ${ \cosh x }$ を使って表されます。

高校時代にどこかで導出を読んだ覚えがあるんですが、その過程で積分方程式が出てきた気がしないので、別の導出方法（ここのものよりも簡単？）もあるかと思います。

準備

ひもの底を原点 ${ O }$ とし、水平方向に ${ x }$ 軸、鉛直方向に ${ y }$ 軸（上方向を正）にとります。　ひもの曲線を ${ y = f(x) }$ とおいて関数 ${ f(x) }$ を求めます。

ひもの ${ x > 0 }$ の部分に点 ${ (x,\,f(x)) }$ をとり、これを ${ P }$ とします。　また、ひもの ${ O }$ から ${ P }$ の部分（両端を含む）を ${ C }$ とします。

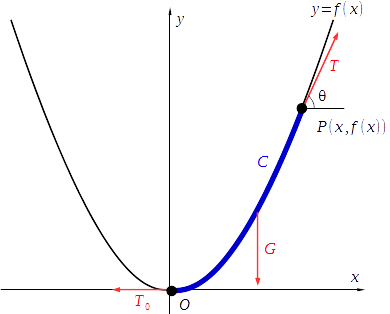
${ f(x) }$ に対する微分方程式を立てる

ひもの一部 ${ C }$ に加わる力の釣り合いの式から ${ f(x) }$ についての微分方程式を立てます。　 ${ C }$ には次の3つの力が加わっています：

点 ${ O }$ に水平方向のひもの張力 ${ T_0 }$
点 ${ P }$ に接線方向上向きにひもの張力 ${ T }$
${ C }$ の重心に鉛直下向きに重力 ${ G }$

${ T_0 }$ は ${ x }$ に無関係な定数です。

${ T }$ について、 ${ P }$ における ${ f(x) }$ の接線と ${ x }$ 軸の正の部分とのなす角を ${ \theta }$ とすると、 ${ T }$ の ${ x }$ 成分、 ${ y }$ 成分はそれぞれ ${ T\cos\theta,\,T\sin\theta }$ となります。　また、この角度 ${ \theta }$ と ${ f(x) }$ は

　　 ${ \displaystyle\begin{align*} f'(x) = \tan\theta \end{align*}}$

で関係しています。　ただし、 ${ ' }$ は ${ x }$ 微分を表します。

${ G }$ は ${ C }$ の長さを ${ \ell }$ , 線密度を ${ \rho }$ 、重力加速度を ${ g }$ として

　　 ${ \displaystyle\begin{align*} G = \rho \ell g \end{align*}}$

で与えられます。　ただし、 ${ C }$ の長さ ${ \ell }$ は ${ f(x) }$ と

　　 ${ \displaystyle\begin{align*} \ell = \int_0^x \sqrt{1+\left\{f'(x)\right\}^2} \,dx \end{align*}}$

で関係しています。

以上の結果を踏まえて、鉛直・水平方向の力の釣り合いの式より

　　 ${ \displaystyle\begin{align*} \begin{cases} \textrm{鉛直方向}: & T \sin\theta = \rho \ell g \\[2mm] \textrm{水平方向}: & T \cos\theta = T_0 \end{cases} \end{align*}}$

となります。　 ${ T }$ を消去して ${ f'(x) = \tan\theta }$ と ${ \ell }$ の式を使うと

　　 ${ \displaystyle\begin{align*} f'(x) &= \frac{\rho g}{T_0} \int_0^x \sqrt{1+\{f'(x)\}^2}\,dx \end{align*}}$

定数をひとまとめにして ${ k = \frac{\rho g}{T_0} }$ とおくと、結局以下の積分方程式が得られます：

　　 ${ \displaystyle\begin{align*} f'(x) &= k \int_0^x \sqrt{1+\{f'(x)\}^2}\,dx \end{align*}}$

これを解くために、微分方程式に書き換えておきましょう。　両辺を ${ x }$ で微分すると

　　 ${ \displaystyle\begin{align*} f''(x) &= k \sqrt{1+\{f'(x)\}^2} \end{align*}}$

概ね「積分方程式 = 微分方程式 + 境界条件」なので境界条件も出しておきましょう。　積分方程式で ${ x = 0 }$ とおいて ${ f'(0) = 0 }$ を得ます。　また、積分方程式からは出てきませんが（ ${ f'(x) }$ しか含んでいないので）、座標系の取り方から ${ f(0) = 0 }$ も境界条件として課されます。　以上をまとめると

　　 ${ \displaystyle\begin{align*} \begin{cases} {\displaystyle f''(x) = k \sqrt{1+\{f'(x)\}^2} } \\[2mm] f(0) = 0, \quad f'(0) = 0 \end{cases} \end{align*}}$

微分方程式を解く

では上記の微分方程式を解いていきましょう。　 ${ z = f'(x) }$ とおくと微分方程式より

　　 ${ \displaystyle\begin{align*} \frac{dz}{dx} &= k\sqrt{1+z^2} \\[2mm] \frac{dz}{\sqrt{1+z^2}} &= k dx \end{align*}}$

となります。　両辺を積分すると、左辺は（以下の ${ \theta }$ は上記で定義した接線に関連する角度と同じですが、単なる置換積分の変数と思って問題ありません）

　　 ${ \displaystyle\begin{align*} \int \frac{dz}{\sqrt{1+z^2}} &= \int \frac{1}{\sqrt{1+\tan^2\theta}}\frac{d\theta}{\cos^2\theta} \qquad \left(z = \tan\theta\right) \\ &= \int \frac{d\theta}{\cos\theta} \\ &= \int \frac{d(\sin\theta)}{\cos^2\theta} \\ &= \frac{1}{2}\int \left(\frac{1}{1-\sin\theta}+\frac{1}{1+\sin\theta}\right)d(\sin\theta) \\ &= \frac{1}{2} \Big\{-\log(1-\sin\theta) + \log(1+\sin\theta)\Big\} \\ &= \frac{1}{2} \log\left(\frac{1+\sin\theta}{1-\sin\theta}\right) \end{align*}}$

また、右辺は簡単に積分できて ${ kx }$ となるので

　　 ${ \displaystyle\begin{align*} \frac{1}{2} \log\left(\frac{1+\sin\theta}{1-\sin\theta}\right) &= kx \\ \frac{1+\sin\theta}{1-\sin\theta} &= e^{2kx} \\ \end{align*}}$

ただし、 ${ f'(x) = z = \tan\theta }$ と境界条件 ${ f'(x) = 0 }$ より、 ${ x = 0 }$ で ${ \theta = 0 }$ なので、積分定数は0になります。

さて、この関係式から ${ \tan\theta \,(= f'(x)) }$ を ${ x }$ で表しましょう。　まずは ${ \sin\theta }$ について解くと

　　 ${ \displaystyle\begin{align*} 1 + \sin\theta &= e^{2kx} (1 - \sin\theta) \\ (e^{2kx} + 1) \sin\theta &= e^{2kx} - 1 \\ \sin\theta &= \frac{e^{2kx} - 1}{e^{2kx} + 1} \quad \left( = \tanh kx\right) \end{align*}}$

次に ${ \tan\theta }$ について解くために公式 ${ 1+\frac{1}{\tan^2\theta} = \frac{1}{\sin^2\theta} }$ （この公式についてはこちらなどを参照）を使うと

　　 ${ \displaystyle\begin{align*} \frac{1}{\tan^2\theta} &= \left(\frac{e^{2kx} + 1}{e^{2kx} - 1}\right)^2 - 1 \\ &= \frac{\left(e^{2kx}+1\right)^2 - \left(e^{2kx}-1\right)^2} {\left(e^{2kx}-1\right)^2} \\ &= \frac{4e^{2kx}}{\left(e^{2kx}-1\right)^2} \\[2mm] \tan\theta &= \frac{e^{2kx}-1}{2\,e^{kx}} \\ &= \frac{e^{kx} - e^{-kx}}{2} \\ &= \sinh kx \end{align*}}$