三角関数の公式を復習する (1) ：三角関数の定義と相互関係

今回から何回かに渡って、高校数学で出てくる三角関数の公式をオイラーの公式を使って定義・導出していきます。

【シリーズ記事の目次】

いくつかの記事は『もう少し三角関数の公式』に移動しました m(_ _)m

【この記事の内容】

定義
- 【発展】その他の三角比（三角関数）
指数関数との関係
- 【発展】その他の三角関数
相互の関係
公式まとめ
- 【追記】

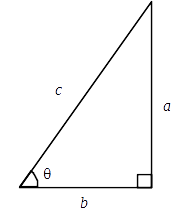
定義

ある直角三角形に対して

斜辺の長さを ${ c }$
直角でない角度の1つを ${ \theta }$
直角と角度 ${ \theta }$ を両端とする方の隣辺*1の長さを ${ b }$
残りの辺の長さを ${ a }$

としたとき（下図参照）、正弦 ${ \sin\theta }$ 、余弦 ${ \cos\theta }$ 、正接 ${ \tan\theta }$ を

　　 ${ \displaystyle\begin{align*} \sin\theta &= \frac{a}{c} & \textrm{（正弦）} \\ \cos\theta &= \frac{b}{c} & \textrm{（余弦）} \\ \tan\theta &= \frac{a}{b} \quad\left(= \frac{\sin\theta}{\cos\theta}\right) & \textrm{（正接）} \end{align*}}$

と定義します。

【発展】その他の三角比（三角関数）

辺の長さが3種あるので、比の取り方は ${ {}_3P_2 = 6 }$ 通りあります。　高校ではこのうち、上記で定義した3種のみが出てきますが、これらの他に

　　 ${ \displaystyle\begin{align*} \cot\theta &= \frac{b}{a} \quad\left(=\frac{1}{\tan\theta}\right) & \textrm{（余接）} \\ \sec\theta &= \frac{c}{b} \quad\left(=\frac{1}{\cos\theta}\right) & \textrm{（正割）} \\ \csc \theta &= \textrm{cosec}\;\theta = \frac{c}{a} \quad\left(=\frac{1}{\sin\theta}\right) & \textrm{（余割）} \end{align*}}$

という三角比があります。

通常、三角関数の表記では ${ \tan^{-1}\theta }$ などは ${ \tan\theta }$ の逆関数（ ${ \textrm{arctan}\;\theta }$ などとも書かれる）として定義されるので、関数値の単なる逆数を表す場合には ${ \frac{1}{\tan\theta} }$ の代わりに ${ \cot\theta }$ と書いたりします。　ただし、多くの場合、高校で出てくる3種の三角比（三角関数）で充分です。

指数関数との関係

高校では学習しませんが、三角関数と指数関数はオイラーの公式

　　 ${ \displaystyle\begin{align*} e^{i\theta} = \cos\theta + i \sin\theta \end{align*}}$

によって関係しています。　ただし ${ i }$ は虚数単位。　この関係を使えば、各三角関数と指数関数との間の関係を導けます：

　　 ${ \displaystyle\begin{align*} \sin x &= \frac{e^{ix} - e^{-ix}}{2i} \\ \cos x &= \frac{e^{ix} + e^{-ix}}{2} \\ \tan x &= \frac{\sin x}{\cos x} = \frac{e^{ix} - e^{-ix}}{e^{ix} + e^{-ix}} = \frac{e^{2ix} -1}{e^{2ix} + 1} \end{align*}}$

【発展】その他の三角関数

高校では出てこない他の3つの三角関数についても指数関数との関係を見ておきましょう：

　　 ${ \displaystyle\begin{align*} \cot x &= \frac{1}{\tan x} = \frac{e^{ix} + e^{-ix}}{e^{ix} - e^{-ix}} = \frac{e^{2ix} + 1}{e^{2ix} -1} \\ \sec x &= \frac{2}{e^{ix} + e^{-ix}} \\ \csc x &= \frac{2i}{e^{ix} - e^{-ix}} \end{align*}}$

相互の関係

ここでは高校数学で出てくる3つの三角関数 ${ \sin x,\,\cos x,\,\tan x }$ についての相互の関係を導きます。　他の3つの三角関数が関わる関係式も同様にして導けますが、特に有用なものはないかと思います。

三平方の定理 ${ a^2 + b^2 = c^2 }$ の両辺を ${ c^2 }$ で割って

　　 ${ \displaystyle\begin{align*} & \left(\frac{a}{c}\right)^2 + \left(\frac{b}{c}\right)^2 = 1 \\ \therefore\, &\sin^2 x + \cos^2 x &= 1 & \cdots(1) \end{align*}}$

また、(1) 式の両辺を ${ \cos^2 x }$ で割ると

　　 ${ \displaystyle\begin{align*} \frac{\sin^2 x}{\cos^2 x} + \frac{\cos^2 x}{\cos^2 x} = \frac{1}{\cos^2 x} \\ \therefore \tan^2 x + 1 = \frac{1}{\cos^2 x} \end{align*}}$

同様に (1) 式の両辺を ${ \sin^2 x }$ で割ると

　　 ${ \displaystyle\begin{align*} 1 + \frac{1}{\tan^2 x} = \frac{1}{\sin^2 x} \end{align*}}$

公式まとめ

定義

　　 ${ \displaystyle\begin{align*} \sin x &= \frac{e^{ix} - e^{-ix}}{2i} & \textrm{（正弦）} \\ \cos x &= \frac{e^{ix} + e^{-ix}}{2} & \textrm{（余弦）} \\ \tan x &= \frac{\sin x}{\cos x} & \textrm{（正接）} \\[4mm] \cot x &= \frac{1}{\tan x} & \textrm{（余接）}\\ \sec x &= \frac{1}{\cos x} & \textrm{（正割）}\\ \csc x &= \frac{1}{\sin x} & \textrm{（余割）}\\ \end{align*}}$

指数関数との関係

　　 ${ \displaystyle\begin{align*} \sin x &= \frac{e^{ix} - e^{-ix}}{2i} \\ \cos x &= \frac{e^{ix} + e^{-ix}}{2} \\ \tan x &= \frac{e^{ix} - e^{-ix}}{e^{ix} + e^{-ix}} = \frac{e^{2ix} -1}{e^{2ix} + 1} \\[4mm] \cot x &= \frac{e^{ix} + e^{-ix}}{e^{ix} - e^{-ix}} = \frac{e^{2ix} + 1}{e^{2ix} -1} \\ \sec x &= \frac{2}{e^{ix} + e^{-ix}} \\ \csc x &= \frac{2i}{e^{ix} - e^{-ix}} \end{align*}}$

相互の関係

　　 ${ \displaystyle\begin{align*} \sin^2 x + \cos^2 x = 1 \\ 1 + \tan^2 x = \frac{1}{\cos^2 x} \\ 1 + \frac{1}{\tan^2 x} = \frac{1}{\sin^2 x} \end{align*}}$