正六面体（立方体）の計量

今回は正六面体（立方体）の表面積や体積など。　5つの正多面体の中で一番簡単。　粛々といきましょう。

幾何学的対象の個数等
隣り合う2つの面のなす角
表面積・体積
内接球・辺に接する球・外接球の半径

一辺の長さを ${ a }$ とし、以下のように頂点に名前を付けておきます。

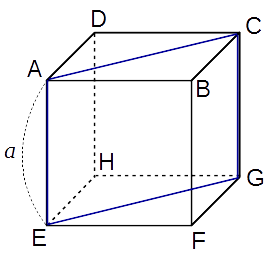
青線で書いた長方形は後で種々の半径を計算するときに使います。

幾何学的対象の個数等

面の数 ${ f }$	6
辺の数 ${ e }$	12
頂点の数 ${ v }$	8
面の形状（正 ${ m }$ 角形）	正方形 ( ${ m = 4 }$ )
1つの頂点に集まる面の個数 ${ p }$	3
双対パートナー	正八面体

オイラーの関係式は

　　 $f - e + v = 6 - 12 + 8 = 2$

となって成り立っています。

正多面体で面の数 ${ f }$ 、面の形状（正 ${ m }$ 角形）、1つの頂点に集まる面の個数 ${ p }$ から辺の数 ${ e }$ と頂点の数 ${ v }$ を計算すると

　　 ${ \displaystyle \begin{align*} e &= \frac{mf}{2} = \frac{4 \cdot 6}{2} = 12 \\ v &= \frac{mf}{p} = \frac{4 \cdot 6}{3} = 8 \end{align*} }$

となり、こちらも成り立っています。

隣り合う2つの面のなす角 ${ \varphi }$

計算するまでも無く

　　 $\varphi = \frac{\pi}{2} = 90^\circ$

ですな。

表面積 ${ S }$ ・体積 ${ V }$

これまた計算するまでもないですね。

　　 ${ \displaystyle \begin{align*} S &= 6a^2 \\ V &= a^3 \end{align*} }$

内接球・辺に接する球・外接球の半径 ${ r,\,\rho,\,R }$

ここまでは（文字で表している以外は）小学校レベルの話だけど、ここからは中3レベルの数学（三平方の定理）が必要。　まぁ、計算式書くほどでもないですが。　上記の図で青色の長方形を書き出すと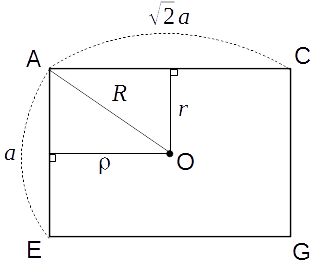
f:id:waman:20150921210258p:plain

対角線 AG の長さが ${ \sqrt{3}a }$ なので

　　 ${ \displaystyle \begin{align*} r &= \frac{1}{2}a \\[2mm] \rho &= \frac{\sqrt{2}}{2}a \\[2mm] R &= \frac{\sqrt{3}}{2}a \end{align*} }$

これらの比は

　　 ${ \displaystyle \begin{align*} r : \rho : R &= \frac{1}{2}a : \frac{\sqrt{2}}{2}a : \frac{\sqrt{3}}{2}a \\ &= 1 : \sqrt{2} : \sqrt{3} \end{align*} }$