高校数学で ζ(1) = ∞ を示す

${ \zeta(x) }$ をリーマンのゼータ関数として、 ${ \zeta (1) }$ は

　　 ${ \displaystyle \begin{align*} \zeta(1) = 1+\frac{1}{2} + \frac{1}{3} + \cdots = \sum_{k=1}^\infty \frac{1}{k} \end{align*} }$

で与えられます。

いろいろ証明の仕方はあるかと思いますが、ここでは数学IIIでよくやる「積分による級数の評価」（正式名称なんだっけ？）を使います。

関数

　　 ${ \displaystyle \begin{align*} y = \frac{1}{x} \end{align*} }$

のグラフとそれに付随する四角の区間の面積を考えて（下図参照）

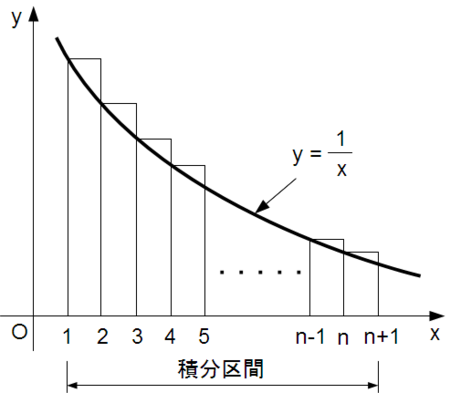
以下の不等式が得られます：

　　 ${ \displaystyle \begin{align*} \sum_{k=1}^n\frac{1}{k} > \sum_{k=1}^n\int_k^{k+1}\frac{dx}{x} = \int_1^{n+1} \frac{dx}{x} \end{align*} }$

ここで最右辺の積分を計算すると

　　 ${ \displaystyle \begin{align*} \int_1^{n+1} \frac{dx}{x} &= \left[\log x\right]_1^{n+1} \\[2mm] &= \log (n+1) \end{align*} }$

となります。　この式で ${ n \rightarrow \infty }$ の極限をとると

　　 ${ \displaystyle \begin{align*} \sum_{k=1}^\infty \frac{1}{k} > \lim_{n\rightarrow\infty}\log(n+1) = \infty \end{align*} }$

よって以下の関係を得ます：

　　 ${ \displaystyle \begin{align*} \sum_{k=1}^\infty \frac{1}{k} =　\infty \end{align*} }$

上の導出の仕方から、発散の仕方が対数的だということも分かりますね。

倭算数理研究所